TEORIA DAS FUNÇÕES

conteúdo ministrado para a primeira série, turmas 11, 12, 13 e 13-A - segundo trimestre.

DEFINIÇÃO

Dados dois conjuntos A e B não vazios , chama-se função (ou aplicação) de A em B, representada por
f : A -> B ; y = f(x) , a qualquer relação binária que associa a cada elemento de A , um único elemento de B.
Portanto , para que uma relação de A em B seja uma função , exige-se que a cada x pertence A esteja associado um único y pertence B , podendo entretanto existir y pertence B que não esteja associado a nenhum elemento pertencente ao conjunto A.

Obs : na notação y = f(x) , entendemos que y é imagem de x pela função f, ou seja:
y está associado a x através da função f.
Exemplo:

f(x) = 4x+3 ; então f(2) = 4.2 + 3 = 11 e portanto , 11 é imagem de 2 pela função f ;
f(5) = 4.5 + 3 = 23 , portanto 23 é imagem de 5 pela função f , f(0) = 4.0 + 3 = 3, etc.
Para definir uma função , necessitamos de dois conjuntos (Domínio e Contradomínio ) e de uma fórmula ou uma lei que relacione cada elemento do domínio a um e somente um elemento do contradomínio .
Quando D(f) C R e CD(f) C R , sendo R o conjunto dos números reais , dizemos que a função f é uma função real de variável real . Na prática , costumamos considerar uma função real de variável real como sendo apenas a lei y = f(x) que a define , sendo o conjunto dos valores possíveis para x , chamado de domínio e o conjunto dos valores possíveis para y , chamado de conjunto imagem da função . Assim , por exemplo , para a função definida por y = 1/x , temos que o seu domínio é D(f) = R* , ou seja o conjunto dos reais diferentes de zero (lembre-se que não existe divisão por zero) , e o seu conjunto imagem é também R* , já que se y = 1/x , então x = 1/y e portanto y também não pode ser zero .
Dada uma função f : A -> B definida por y = f(x) , podemos representar os pares ordenados (x , y) E f onde x C A e y E B ,num sistema de coordenadas cartesianas .
O gráfico obtido será o gráfico da função f .

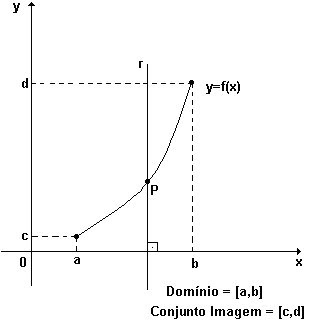
Assim , por exemplo , sendo dado o gráfico cartesiano de uma função f , podemos dizer que:
a ) a projeção da curva sobre o eixo dos x , nos dá o domínio da função .

b ) a projeção da curva sobre o eixo dos y , nos dá o conjunto imagem da função .

c ) toda reta vertical que passa por um ponto do domínio da função , intercepta o gráfico da função em no máximo um ponto .
Veja a figura abaixo:


Tipos de funções
Função sobrejetora
É aquela cujo conjunto imagem é igual ao contradomínio .
Exemplo:


Função injetora
Uma função y = f(x) é injetora quando elementos distintos do seu domínio , possuem imagens distintas,
isto é:
x1 # x2 => f(x1) # f(x2) # x2 => f(x1) # f(x2) # x2 => f(x1) # f(x2) # x2 => f(x1) # f(x2) # x2 => f(x1) # f(x2) # x2 => f(x1) # f(x2) # x2 => f(x1) # f(x2) .(# siginifica diferente)
Exemplo:

Função bijetora
Uma função é dita bijetora , quando é ao mesmo tempo , injetora e sobrejetora .
Exemplo:







Exercícios resolvidos:
1 - Considere três funções f, g e h, tais que:
A função f atribui a cada pessoa do mundo, a sua idade.
A função g atribui a cada país, a sua capital
A função h atribui a cada número natural, o seu dobro.
Podemos afirmar que, das funções dadas, são injetoras:
a) f, g e h
b) f e h
c) g e h
d) apenas h
e) nenhuma delas
Solução:

Sabemos que numa função injetora, elementos distintos do domínio, possuem imagens distintas, ou seja:
x1 # x2 -> f(x1) # f(x2) .
Logo, podemos concluir que:

f não é injetora, pois duas pessoas distintas podem ter a mesma idade.
g é injetora, pois não existem dois países distintos com a mesma capital.
h é injetora, pois dois números naturais distintos, possuem os seus dobros também distintos.
Assim é que concluímos que a alternativa correta é a de letra C.
2 - Seja f uma função definida em R - conjunto dos números reais - tal que
f(x - 5) = 4x. Nestas condições, pede-se determinar f(x + 5).
Solução:

Vamos fazer uma mudança de variável em f(x - 5) = 4x, da seguinte forma:
x - 5 = u logo x = u + 5

Substituindo agora (x - 5) pela nova variável u e x por (u + 5), vem:
f(u) = 4(u + 5) logo f(u) = 4u + 20
Ora, se f(u) = 4u + 20, teremos:
f(x + 5) = 4(x+5) + 20 Então f(x+5) = 4x + 40

Agora resolva este:

A função f em R é tal que f(2x) = 3x + 1. Determine 2.f(3x + 1).
Resp: 9x + 5
3 - Paridade das funções
3.1 - Função par
A função y = f(x) é par, quando  x qualquer que seja D(f) , f(- x ) = f(x) , ou seja, para todo elemento do seu domínio,
f( x ) = f ( - x ). Portanto , numa função par, elementos simétricos possuem a mesma imagem. Uma conseqüência desse fato é que os gráficos cartesiano das funções pares, são curvas simétricas em relação ao eixo dos y ou eixo das ordenadas.
Exemplo:
y = x4 + 1 é uma função par, pois f(x) = f(-x), para todo x. Por exemplo,
f(2) = 24 + 1 = 17 e f(- 2) = (-2)4 + 1 = 17
O gráfico abaixo, é de uma função par.


Função ímpar
A função y = f(x) é ímpar , quando qualquer que seja x E D(f) , f( - x ) = - f (x) , ou seja, para todo elemento do seu domínio, f( - x) = - f( x ). Portanto, numa função ímpar, elementos simétricos possuem imagens simétricas. Uma conseqüência desse fato é que os gráficos cartesianos das funções ímpares, são curvas simétricas em relação ao ponto (0,0), origem do sistema de eixos cartesianos.
Exemplo:

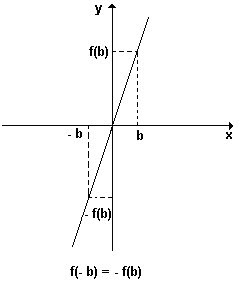
y = x3 é uma função ímpar pois para todo x, teremos f(- x) = - f(x).
Por exemplo, f( - 2) = (- 2)3 = - 8 e - f( x) = - ( 23 ) = - 8.
O gráfico abaixo é de uma função ímpar:


Nota: se uma função y = f(x) não é par nem ímpar, dizemos que ela não possui paridade.

Exemplo:

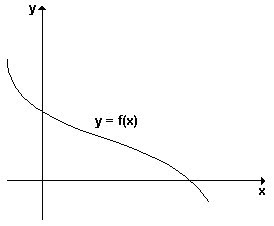
O gráfico abaixo, representa uma função que não possui paridade, pois a curva não é simétrica em relação ao eixo dos x e, não é simétrica em relação à origem.

1 - FUNÇÃO INVERSA
Dada uma função f : A -> B , se f é bijetora , então define-se a função inversa f -1 como sendo a função de B em A , tal que f-1 (y) = x .
Veja a representação a seguir:


É óbvio então que:
a) para obter a função inversa , basta permutar as variáveis x e y .
b) o domínio de f -1 é igual ao conjunto imagem de f .
c) o conjunto imagem de f -1 é igual ao domínio de f .
d) os gráficos de f e de f -1 são curvas simétricas em relação à reta y = x ou seja , à bissetriz do primeiro quadrante .
Exemplo:
Determine a INVERSA da função definida por y = 2x + 3.
Permutando as variáveis x e y, fica: x = 2y + 3
Explicitando y em função de x, vem:
2y = x - 3 então y = (x - 3) / 2, que define a função inversa da função dada.
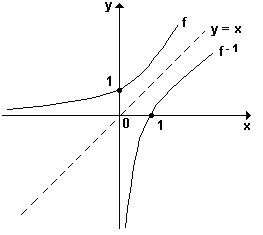
O gráfico abaixo, representa uma função e a sua inversa.
Observe que as curvas representativas de f e de f-1, são simétricas em relação à reta
y = x, bissetriz do primeiro e terceiro quadrantes.



Exercício resolvido:
A função f: R -> R , definida por f(x) = x2 :
a) é inversível e sua inversa é f -1 (x) = Raiz de x
b) é inversível e sua inversa é f -1(x) = - Raiz de x
c) não é inversível
d) é injetora
e) é bijetora
SOLUÇÃO:
Já sabemos que somente as funções bijetoras são inversíveis, ou seja, admitem função inversa. Ora, a função f(x) = x2, definida em R - conjunto dos números reais - não é injetora, pois elementos distintos possuem a mesma imagem. Por exemplo,
f(3) = f(-3) = 9. Somente por este motivo, a função não é bijetora e, em conseqüência, não é inversível.
Observe também que a função dada não é sobrejetora, pois o conjunto imagem da função f(x) = x2 é o conjunto R + dos números reais não negativos, o qual não coincide com o contradomínio dado que é
igual a R. A alternativa correta é a letra C.
2 - FUNÇÃO COMPOSTA
Chama-se função composta ( ou função de função ) à função obtida substituindo-se a variável independente x , por uma função.
Simbologia : fog (x) = f(g(x)) ou gof (x) = g(f(x)) .
Veja o esquema a seguir:


Obs : atente para o fato de que fog # gof , ou seja, a operação " composição de funções " não é comutativa .
Exemplo:
Dadas as funções f(x) = 2x + 3 e g(x) = 5x, pede-se determinar gof(x) e fog(x).
Teremos:
gof(x) = g[f(x)] = g(2x + 3) = 5(2x + 3) = 10x + 15
fog(x) = f[g(x)] = f(5x) = 2(5x) + 3 = 10x + 3
Observe que fog # gof .
Exercícios resolvidos:
1 - Sendo f e g duas funções tais que: f(x) = ax + b e g(x) = cx + d . Podemos afirmar que a igualdade gof(x) = fog(x) ocorrerá se e somente se:
a) b(1 - c) = d(1 - a)
b) a(1 - b) = d(1 - c)
c) ab = cd
d) ad = bc
e) a = bc
SOLUÇÃO:
Teremos:
fog(x) = f[g(x)] = f(cx + d) = a(cx + d) + b então fog(x) = acx + ad + b
gof(x) = g[f(x)] = g(ax + b) = c(ax + b) + d então gof(x) = cax + cb + d
Como o problema exige que gof = fog, fica:
acx + ad + b = cax + cb + d
Simplificando, vem:
ad + b = cb + d
ad - d = cb - b então d(a - 1) = b(c - 1), que é equivalente a d(a - 1) = b(c - 1), o que nos leva a concluir que a alternativa correta é a letra A. .
2 - Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:
a) 2 - 2x
b) 3 - 3x
c) 2x - 5
*d) 5 - 2x
e) uma função par.
SOLUÇÃO:
Sendo fog(x) = 2x + 1, temos: f[g(x)] = 2x + 1
Substituindo g(x) pelo seu valor, fica: f(2 - x) = 2x + 1
Fazendo uma mudança de variável, podemos escrever 2 - x = u, sendo u a nova variável. Portanto, x = 2 - u.
Substituindo, fica:
f(u) = 2(2 - u) + 1 então f(u) = 5 - 2u
Portanto, f(x) = 5 - 2x , o que nos leva à alternativa D.
Agora resolva esta:
Dadas as funções f(x) = 4x + 5 e g(x) = 2x - 5k, ocorrerá gof(x) = fog(x) se e somente se k for igual a:
*a) -1/3
b) 1/3
c) 0
d) 1
e) -1
Tipos particulares de funções
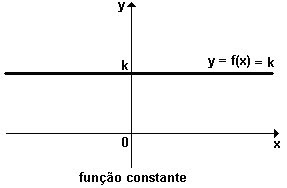
FUNÇÃO CONSTANTE
Uma função é dita constante quando é do tipo f(x) = k , onde k não depende de x .
Exemplos:
a) f(x) = 5
b) f(x) = -3
Obs : o gráfico de uma função constante é uma reta paralela ao eixo dos x .
Veja o gráfico a seguir:



FUNÇÃO DO 1º GRAU
Uma função é dita do 1º grau , quando é do tipo y = ax + b , onde a # 0 .
Exemplos :
f(x) = 3x + 12 ( a = 3 ; b = 12 )
f(x) = -3x + 1 (a = -3; b = 1).
Propriedades da função do 1º grau :
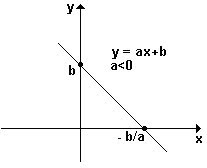
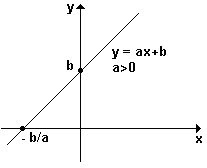
1) o gráfico de uma função do 1º grau é sempre uma reta










2) na função f(x) = ax + b , se b = 0 , f é dita função linear e se b # 0 f é dita função afim .
3) o gráfico intercepta o eixo dos x na raiz da equação f(x) = 0 e, portanto, no ponto de abcissa x = - b/a .
4) o gráfico intercepta o eixo dos y no ponto (0 , b) , onde b é chamado coeficiente linear .
5) o valor a é chamado coeficiente angular e dá a inclinação da reta .
6) se a > 0 , então f é crescente .
7) se a < 0 , então f é decrescente .
8) quando a função é linear, ou seja, y = f(x) = ax , o gráfico é uma reta que sempre passa na origem.
Exercício resolvido:
1 - Determine a função f(x) = ax + b, sabendo-se que f(2) = 5 e f(3) = -10.
SOLUÇÃO:
Podemos escrever:
5 = 2.a + b
-10 = 3.a + b
Subtraindo membro a membro, vem:
5 - (- 10) = 2.a + b - (3.a + b)
15 = - a então a = - 15
Substituindo o valor de a na primeira equação (poderia ser na segunda), fica:
5 = 2.(- 15) + b então b = 35.
Logo, a função procurada é: y = - 15x + 35.
Agora resolva esta:
A função f é definida por f(x) = ax + b. Sabe-se que f(-1) = 3 e f(3) = 1, então podemos afirmar que f(1) é
igual a:
*a) 2
b) -2
c) 0
d) 3
e) -3
FUNÇÃO DO 2º GRAU
Uma função é dita do 2º grau quando é do tipo f(x) = ax2 + bx + c , com a # 0 .
Exemplos: f(x) = x2 - 2x + 1 ( a = 1 , b = -2 , c = 1 ) ;
y = - x2 ( a = -1 , b = 0 , c = 0 )
Gráfico da função do 2º grau y = ax2 + bx + c :
é sempre uma parábola de eixo vertical .














Propriedades do gráfico de y = ax2 + bx + c :
1) se a > 0 a parábola tem um ponto de mínimo .
2) se a < 0 a parábola tem um ponto de máximo
3) o vértice da parábola é o ponto V(xv , yv) onde:
xv = - b/2a
yv = - Delta /4a , onde Delta = b2 - 4ac
4) a parábola intercepta o eixo dos x nos pontos de abcissas x' e x'' , que são as raízes da
equação ax2 + bx + c = 0 .
5) a parábola intercepta o eixo dos y no ponto (0 , c) .
6) o eixo de simetria da parábola é uma reta vertical de equação x = - b/2a.
7) Ymax = - Delta / 4a ( a < 0 )
8) Ymin = - Delta /4a ( a > 0 )
9) Im(f) = { y E R ; y > - Delta /4a } ( a >0 )
10) Im(f) = { y E R ; y < - Delta /4a} ( a < 0)
11) Forma fatorada : sendo x1 e x2 as raízes da de f(x) = ax2 + bx + c , então ela pode ser escrita na forma fatorada a seguir :
y = a(x - x1).(x - x2)