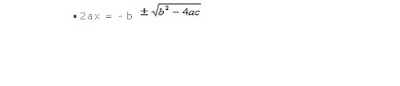O hábito de dar nome de Bhaskara para a fórmula de resolução da equação de 2ºgrau se estabeleceu no Brasil por volta de 1960. Esse costume, aparentemente só brasileiro (não se encontra o nome de Bhaskara para essa fórmula na literatura internacional), não é adequado, pois:
Problemas que recaem numa equação de 2º grau já apareciam, há quase 4.000 anos, em textos escritos pelos babilônicos. Nestes textos o que se tinha era uma receita (escrita em prosa, sem uso de símbolos) que ensinava como proceder para determinar as raízes em exemplos concretos com coeficientes numéricos;
Bhaskara que nasceu na Índia em 1.114 e viveu cerca de 1.185 e foi um dos mais importantes matemáticos do século XII. As duas coleções de seus trabalhos mais conhecidas são Lilavati ("bela") e Vijaganita ("extração de raízes"), que tratam de aritmética e álgebra respectivamente, e contêm numerosos problemas sobre equações de lineares e quadráticas (resolvidas também com receitas em prosa), progressões aritméticas e geométricas, radicais, tríadas pitagóricas e outros.
Até o fim do século XVI não se usava uma fórmula para obter as raízes de uma equação do 2º grau, simplesmente porque não se representavam por letras os coeficientes de uma equação. Isso só começou a ser feito a partir da François Viéte, matemático francês que viveu de 1540 a 1603.
Logo, embora não se deva negar a importância e a riqueza da obra de Bhaskara, não é correto atribuir a ele a conhecida fórmula de resolução da equação de 2º grau.
A FÓRMULA DA EQUAÇÃO DO 2º GRAU
A ideia é completar o trinômio ax2 + bx + c de modo a fatorá-lo num quadrado perfeito:
ax² + bx + c = 0, inicialmente multiplicamos a igualdade por 4a,
4a²x² + 4abx + 4ac = 0, agora somamos b2 aos dois lados da igualdade:
· 4a²x² + 4abx + 4ac + b² = b²
Passamos 4ac para o segundo membro
· 4a²x² + 4abx + b² = b² - 4ac
Fatoramos o trinômio 4a2x2 + 4abx + b2
· (2ax + b) 2 = b2 - 4ac
Utilizamos a operação inversa da potenciação
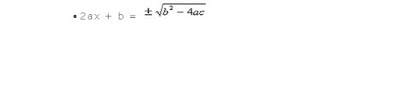
· 2ax + b =
Passamos o termo b para o segundo membro
· 2ax = - b
Passamos 2a para o segundo termo usando a operação inversa
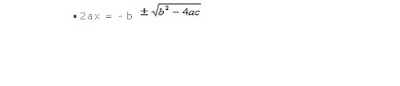
Obtemos a fórmula para calcularar as raízes de uma equação do 2º grau.

Fontes:
www.sandroatini.sites.uol.com.br/bhaskara.htm
Revista do Professor de Matemática - nº 39