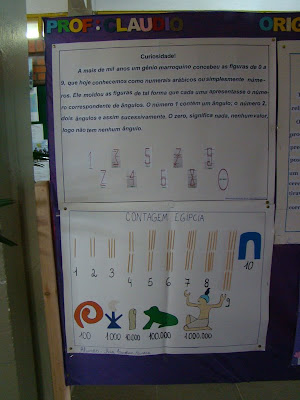
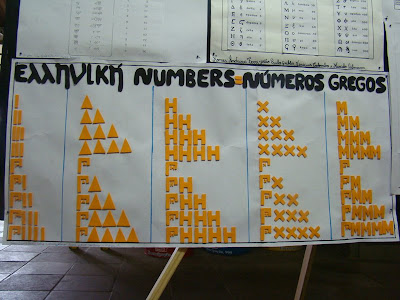
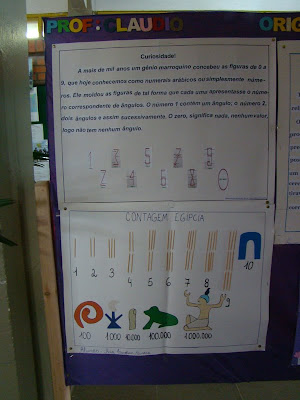
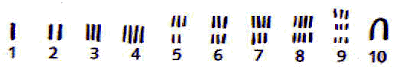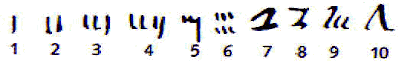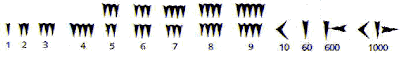O conjunto dos números naturais é representado pela letra maiúscula N e estes números são construídos com os algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, que também são conhecidos como algarismos indo-arábicos.
No século VII, os árabes invadiram a Índia, difundindo o seu sistema numérico.
Embora o zero não seja um número natural no sentido que tenha sido proveniente de objetos de contagens naturais, iremos considerá-lo como um número natural uma vez que ele tem as mesmas propriedades algébricas que os números naturais. Na verdade, o zero foi criado pelos hindus na montagem do sistema posicional de numeração para suprir a deficiência de algo nulo.
Na sequência abaixo consideraremos como naturais tendo início com o número zero e escreveremos este conjunto como:
N = { 0, 1, 2, 3, 4, 5, 6, ...}
Representaremos o conjunto dos números naturais com a letra N. As reticências (três pontos) indicam que este conjunto não tem fim. N é um conjunto com infinitos números.
Excluindo o zero do conjunto dos números naturais, o conjunto será representado por N*, isto é:
N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
A construção dos Números Naturais
Todo número natural dado tem um sucessor (número que vem depois do número dado), considerando também o zero.
Exemplos:
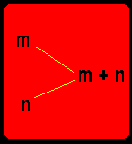
O sucessor de m é m + 1 se, m é um número natural.
O sucessor de 0 é 1.
O sucessor de 1 é 2.
O sucessor de 19 é 20.
Se um número natural é sucessor de outro, então os dois números juntos são chamados números consecutivos.
Exemplos:
1 e 2 são números consecutivos
5 e 6 são números consecutivos
50 e 51 são números consecutivos
Vários números formam uma colecção de números naturais consecutivos se o segundo é sucessor do primeiro, o terceiro é sucessor do segundo, o quarto é sucessor do terceiro e assim sucessivamente.
Exemplos:
1, 2, 3, 4, 5, 6, 7 e 8 são números consecutivos
5, 6 e 7 são números consecutivos
50, 51, 52 e 53 são números consecutivos
Todo número natural dado n, exceto o zero, tem um antecessor (número que vem antes do número dado).
Exemplos:
O antecessor de m é m-1 se, m é um número natural finito diferente de zero.
O antecessor de 2 é 1.
O antecessor de 56 é 55.
O antecessor de 10 é 9.
O conjunto abaixo é conhecido como o conjunto dos números naturais pares.
Embora uma sequência real seja um outro objeto matemático denominado função, algumas vezes utilizaremos a denominação sequência dos números naturais pares para representar o conjunto dos números naturais pares:
P = { 0, 2, 4, 6, 8, 10, 12, ...}
O conjunto abaixo é conhecido como o conjunto dos números naturais ímpares, às vezes também chamado, a sequência dos números ímpares.
I = { 1, 3, 5, 7, 9, 11, 13, ...}
Igualdades e Desigualdades
Diremos que um conjunto A é igual a um conjunto B se, e somente se, o conjunto A está contido no conjunto B e o conjunto B está contido no conjunto A. Quando a condição acima for satisfeita, escreveremos A=B (lê-se: A é igual a B) e quando não for satisfeita denotaremos tal fato por:

(lê-se: A é diferente de B). Na definição de igualdade de conjuntos, vemos que não é importante a ordem dos elementos no conjunto.
Exemplo com igualdade:
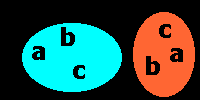
Notamos que os elementos do conjunto A são os mesmos elementos do conjunto B. Neste caso, A=B.
Vamos considerar agora uma situação em que os elementos dos conjuntos A e B serão distintos. Neste caso, dizemos que A é diferente de B.
Sejam A = {a,b,c,d} e B = {1,2,3,d}. Estes conjuntos são diferentes pois nem todos os elementos do conjunto A estão em B e nem todos os elementos do conjunto B estão em A.
Não podemos afirmar que um conjunto é maior do que o outro conjunto.
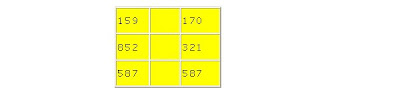
Exercício: Coloque um dos três sinais: <, > ou = em cada linha da tabela abaixo.
Exercício: Representar cada conjunto analiticamente, isto é, através de alguma propriedade e depois por extensão, apresentando os elementos:
N : Conjunto dos Números Naturais
P : Conjunto dos Números Naturais Pares
I : Conjunto dos Números Naturais Ímpares
E : Conjunto dos Números Naturais menores que 16
L : Conjunto dos Números Naturais maiores que 11
R : Conjunto dos Números Naturais maiores ou iguais a 28
C : Conjunto dos Números Naturais que estão entre 6 e 10
A adição de números naturais
A primeira operação fundamental da Aritmética, tem por finalidade reunir em um só número, todas as unidades de dois ou mais números. Antes de surgir os algarismos indo-arábicos, as adições podiam ser realizadas por meio de tábuas de calcular, com o auxílio de pedras ou por meio de ábacos.

Propriedades da Adição
Fechamento
A adição é fechada no conjunto dos números naturais, pois a soma de dois números naturais é ainda um número natural. O facto que a operação de adição é fechada em N é conhecido na literatura do assunto como:
A adição é uma lei de composição interna no conjunto N.
Associativa
A adição é associativa no conjunto dos números naturais, pois na adição de três ou mais parcelas de números naturais quaisquer é possível associar as parcelas de quaisquer modos, ou seja, com três números naturais, somando o primeiro com o segundo e ao resultado obtido somarmos um terceiro, obteremos um resultado que é igual à soma do primeiro com a soma do segundo e o terceiro.
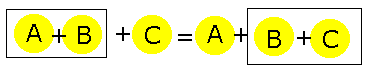
Elemento neutro
Na adição de números naturais, existe o elemento neutro que é o zero, pois tomando um número natural qualquer e somando com o elemento neutro (zero), o resultado será o próprio número natural
.

Comutativa
A adição é comutativa no conjunto dos números naturais, pois a ordem das parcelas não altera a soma, ou seja, somando a primeira parcela com a segunda parcela, teremos o mesmo resultado que se somando a segunda parcela com a primeira parcela.

Curiosidade: Tabela de adição
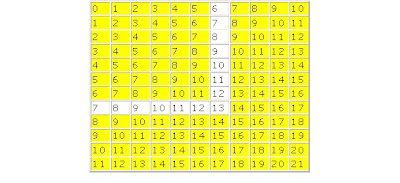
Para somar dois números com a tabela em anexo, basta fixar um número na primeira linha e um segundo número na primeira coluna e na intersecção da linha com a coluna fixadas, obtemos a soma desses números.
Como exemplo, na tabela ao lado, se tomamos o número 7 que está na linha horizontal e o número 6 que está na linha vertical, obteremos a soma 13 que está no cruzamento das duas linhas.
Multiplicação de Números Naturais
É a operação que tem por finalidade adicionar o primeiro número denominado multiplicando ou parcela, tantas vezes quantas são as unidades do segundo número denominado multiplicador.
Exemplo: 4 vezes 9 é somar o número 9 quatro vezes:
4 x 9 = 9 + 9 + 9 + 9 = 36
O resultado da multiplicação é denominado produto e os números dados que geraram o produto, são chamados fatores. Usamos o sinal x ou · ou × para representar a multiplicação.
Propriedades da multiplicação
Fechamento
A multiplicação é fechada no conjunto N dos números naturais, pois realizando o produto de dois ou mais números naturais, o resultado estará em N. O fato que a operação de multiplicação é fechada em N é conhecido na literatura do assunto como:
A multiplicação é uma lei de composição interna no conjunto N.
Associativa
Na multiplicação, podemos associar 3 ou mais factores de modos diferentes, pois se multiplicarmos o primeiro fator com o segundo e depois multiplicarmos por um terceiro número natural, teremos o mesmo resultado que multiplicar o terceiro pelo produto do primeiro pelo segundo.
(m.n).p = m.(n.p)
(3.4).5 = 3.(4.5) = 60
Elemento Neutro
No conjunto dos números naturais existe um elemento neutro para a multiplicação que é o 1. Qualquer que seja o número natural n, tem-se que:
1.n = n.1 = n
1.7 = 7.1 = 7
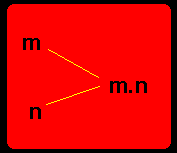
Comutativa
Na multiplicação de dois números naturais quaisquer, a ordem dos fatores não altera o produto, ou seja, multiplicando o primeiro elemento pelo segundo elemento teremos o mesmo resultado que se multiplicarmos o segundo elemento pelo primeiro elemento.
m.n = n.m
3.4 = 4.3 = 12
Propriedade Distributiva
Multiplicando um número natural pela soma de dois números naturais, é o mesmo que multiplicar o fator, por cada uma das parcelas e a seguir adicionar os resultados obtidos.

m . ( p + q ) = m . p + m . q
6 x ( 5 + 3 ) = 6 x 5 + 6 x 3 = 30 + 18 = 48
Divisão de Números Naturais
Dados dois números naturais, às vezes necessitamos saber quantas vezes o segundo está contido no primeiro. O primeiro número que é o maior é denominado dividendo e o outro número que é menor é o divisor. O resultado da divisão é chamado quociente. Se multiplicarmos o divisor pelo quociente obteremos o dividendo.
No conjunto dos números naturais, a divisão não é fechada, pois nem sempre é possível dividir um número natural por outro número natural e na ocorrência disto a divisão não é exata.
Relações essenciais numa divisão de números naturais
Numa divisão de números naturais, o divisor deve ser menor do que o dividendo.
35 : 7 = 5
Numa divisão de números naturais, o dividendo é o produto do divisor pelo quociente.
35 = 5 x 7
A divisão de um número natural n por zero não tem sentido pois, se admitíssemos que o quociente fosse q, então poderíamos escrever:
n ÷ 0 = q
e isto significa que:
n = 0 x q = 0
o que não é correto, logo a divisão de n por 0 não tem sentido ou ainda é dita impossível.
Exercício: Substituindo X por 6 e Y por 9, qual o valor da soma do dobro de X pelo triplo de Y.
Potenciação de Números Naturais
Dados dois números naturais x e y, a expressão xy, representa um produto de y fatores iguais ao número x, ou seja:
xy = x . x . x . x ... x . x . x
y vezes
O número que se repete como fator denomina-se base que neste caso é x. O número de vezes que a base se repete é denominado expoente que neste caso é y. O resultado denomina-se potência. Esta operação não passa de uma multiplicação com fatores iguais.
Exemplos:
23 = 2 . 2 . 2 = 8
43 = 4 . 4 . 4 = 64
Propriedades da Potenciação
Uma potência cuja base é igual a 1 e o expoente natural é n, denotado por 1n, será sempre igual a 1.
Exemplos:
1n = 1 . 1 ... 1 (n vezes) = 1
13 = 1 . 1 . 1 = 1
17 = 1 . 1 . 1 . 1 . 1 . 1 . 1 = 1
Se n é um número natural diferente de zero, então a potência no será sempre igual a 1.
Exemplos:
no = 1
5o = 1
49o = 1
Qualquer que seja a potência em que a base é o número natural n e o expoente é igual a 1, denotado por n1 é igual ao próprio n.
Exemplos:
n1 = n
51 = 5
641 = 64
Toda potência 10n é o número formado pelo algarismo 1 seguido de n zeros.
Exemplos:
103 = 1000
108 = 100.000.000
10o = 1
CURIOSIDADENúmeros grandes
No livro "Matemática e Imaginação", o matemático americano Edward Kasner apresentou um número denominado googol que pode ser representado por 1 seguido de 100 zeros.
1 Googol = 10100
Ele pensou que este era um número superior a qualquer coisa que passasse pela mente humana sendo maior do que qualquer coisa que pode ser posta na forma de palavras. Um googol é um pouco maior do que o número total de partículas elementares conhecidas no universo, algo da ordem de 1080. Se o espaço com estas partículas fosse comprimido de uma forma sólida com neutrões, este ficaria com algo em torno de 10128 partículas.
Um outro matemático criou então o googolplex e o definiu como sendo 10 elevado ao googol.
1 Googolplex = 10Googol = 1010100
Múltiplos de números Naturais
Diz-se que um número natural a é múltiplo de outro natural b, se existe um número natural k tal que:
a=k.b
Exemplos:
15 é múltiplo de 5, pois 15 = 3 x 5
24 é múltiplo de 4, pois 24 = 6 x 4
24 é múltiplo de 6, pois 24 = 4 x 6
27 é múltiplo de 9, pois 27 = 3 x 9
Quando a = k . b, segue que a é múltiplo de b, mas também, a é múltiplo de k, como é o caso do número 35 que é múltiplo de 5 e de 7, pois:
35 = 7 x 5
Quando a=k.b, então a é múltiplo de b e se conhecemos b e queremos obter todos os seus múltiplos, basta fazer k assumir todos os números naturais possíveis. Para obter os múltiplos de 2, isto é, os números da forma a=kx2 onde k é substituído por todos os números naturais possíveis. A tabela abaixo nos auxiliará:
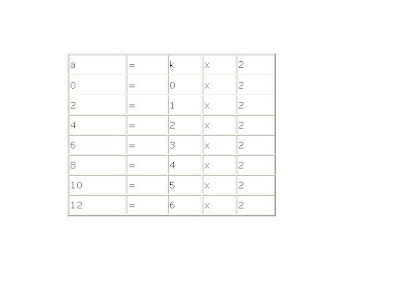
O conjunto dos números naturais é infinito, assim existem infinitos múltiplos de 2, ou de qualquer outro número natural.
O conjunto dos múltiplos de um número natural y é infinito e vamos nos referir a este conjunto com a notação M(y).
Exemplo: Múltiplos de 7: M(7) = {0,7,14,21,28,35,42,...}

Exemplo: Múltiplos de 11: M(11) = {0,11,22,33,44,55,66,77,...}

Observação: Como estamos considerando 0 como um número natural, então o número 0 (zero) será múltiplo de todo número natural. Tomando k=0 em a=k.b obtemos a=0 para todo b natural.
Exemplo: Alguns múltiplos de zero.
0 = 0 x 2
0 = 0 x 5
0 = 0 x 12
0 = 0 x 15
Observação: Um número b é sempre múltiplo dele mesmo.
a = 1 x b <=> a = b
Exemplos: Basta tomar o mesmo número multiplicado por 1 para obter um múltiplo dele próprio.
3 = 1 x 3
5 = 1 x 5
15 = 1 x 15
Divisores de números Naturais
A definição de divisor está relacionada com a de múltiplo. Um número natural b é divisor do número natural a, se a é múltiplo de b.
Exemplo: 3 é divisor de 15, pois 15=3x5, logo 15 é múltiplo de 3 e também é múltiplo de 5.
Um número natural tem uma quantidade finita de divisores. Por exemplo, o número 6 poderá ter no máximo 6 divisores, pois trabalhando no conjunto dos números naturais não podemos dividir 6 por um número maior do que ele.
Os divisores naturais de 6 são os números 1, 2, 3, 6, o que significa que o número 6 tem 4 divisores.
Os divisores de um número y também formam um conjunto finito, que aqui denotaremos por D(y).
Exemplos:
Divisores de 18: D(18) = { 1, 2, 3, 6, 9, 18 }
Divisores de 15: D(15) = { 1, 3, 5, 15 }
Observação:
O número 0(zero) é múltiplo de todo número natural.
Zero(0) não é divisor de nenhum número natural, exceto dele próprio.
Se pudéssemos considerar que 6÷0=b, então teríamos que admitir que:
6 = 0 x b
mas não existe um número b que multiplicado por 0 (zero) seja igual a 6, portanto a divisão de 6 por 0 é impossível.
A divisão de zero por zero é indeterminada, o que significa que pode existir uma situação que ela passe a ter significado, no sentido seguinte:
Se aceitarmos que
0 ÷ 0 = X ÷ 1 = X
então também poderemos aceitar que o produto dos meios é igual ao produto dos extremos nesta proporção e assim:
0 × 1 = 0 × X = 0
que não é contraditório e isto pode ser realizado para todo X real, razão pela qual a expressão da forma 0 ÷ 0 é dita indeterminada.
Números primos
Um número primo é um número natural com exatamente dois divisores naturais distintos.
Exemplos:
2 é primo pois D(2) = {1,2}
3 é primo pois D(3) = {1,3}
5 é primo pois D(5) = {1,5}
7 é primo pois D(7) = {1,7}
14 não é primo pois D(14) = {1,2,7,14}
Crivo de Eratóstenes É um processo para a obtenção de números primos menores do que um determinado número natural k. Normalmente construímos uma tabela contendo todos os primeiros k números naturais.
Para determinar os números primos nesta tabela, basta seguir os seguintes passos.
Determinamos o primeiro número primo que é 2, lembrando que 1 não é primo.
Eliminamos todos os múltiplos de 2 que encontrarmos na tabela.
Determinamos o próximo número primo que será 3, que coincidirá com o próximo número não marcado da tabela.
Eliminamos todos os múltiplos de 3.
Voltamos ao passo 3, com o próximo número primo.
Continuamos o processo.

Na tabela, listamos os 100 primeiros números naturais, indicando com a cor de fundo "amarela" os números primos e com a cor de fundo "verde" os números que não são primos. Como exemplo, 2 é primo, enquanto 25 não é primo, pois é múltiplo de 5.
Assim encontramos os seguintes números primos na tabela.
P={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}
Observações:
1 não é primo pois tem apenas 1 divisor.
Todo número natural pode ser escrito como o produto de números primos, de forma única.
Mínimo Múltiplo Comum
Diz-se que um número m é múltiplo comum dos número a e b se m é múltiplo de a e também é múltiplo de b, ou seja.
m = k . a
e
m = w . b
onde k e w números naturais.
Exemplos: Múltiplos comuns
24 é múltiplo comum de 6 e 8.
15 é múltiplo comum de 3 e 5.
Determinaremos agora todos os números que tem 18 como múltiplo comum, o que é o mesmo que obter todos os divisores naturais de 18.
18 é múltiplo comum de 1 e 18 pois 18=1x18.
18 é múltiplo comum de 2 e 9 pois 18=2x9.
18 é múltiplo comum de 3 e 6 pois 18=3x6.
Observe que 18 é múltiplo comum de todos os seus divisores, logo:
D(18) = {1,2,3,6,9,18}
Agora determinaremos os múltiplos comuns dos números a e b. Para isso denotaremos por M(a) o conjunto dos múltiplos de a, por M(b) o conjunto dos múltiplos de b e tomar a intersecção entre os conjuntos M(a) e M(b).
Exemplo: Múltiplos comuns de 3 e 5.
M(3)={0,3,6,9,12,15,18,21,24,27,30,33,36,39,42,45,...}
M(5)={0,5,10,15,20,25,30,35,40,45,50,55,...}
Desse modo, a intersecção entre os conjuntos M(3) e M(5) forma um conjunto infinito com os múltiplos comuns de 3 e de 5.
M(3)M(5) = {0,15,30,45,...}
Como estamos considerando 0 (zero) como número natural, ele irá fazer parte dos conjuntos de todos os múltiplos de números naturais e será sempre o menor múltiplo comum.
Por definição, o Mínimo Múltiplo Comum (MMC) de dois ou mais números naturais é o menor múltiplo comum a esses números que é diferente de zero. Logo, no conjunto:
M(3)M(5) = {0, 15, 30, 45, ...}
o Mínimo Múltiplo Comum entre 3 e 5 é igual a 15.
Quando trabalharmos com dois números a e b, utilizaremos a notação MMC(a,b) para representar o Mínimo Múltiplo Comum entre os números naturais a e b, lembrando sempre que o menor múltiplo comum deve ser diferente de zero.
Exemplo: Como:
M(4) = {0,4,8,12,16,20,24,...}
M(6) = { 0, 6, 12, 18, 24, ...}
então:
MMC(4,6) = min {12,24,36,...} = 12
É interessante notar que o conjunto dos múltiplos do MMC(a,b) é igual ao conjunto dos múltiplos comuns de a e b.
Realmente: MMC(3,5)=15
M(15) = {0,15,30,45,60,...}
M(3) = {0,3,6,9,12,15,18,21,24,27,30,...}
M(5) = {0,5,10,15,20,25,30,35,40,45,...}
M(3)M(5) = {0,15,30,45,...}
Observe que M(15) = M(3)M(5)
Método para determinar o MMC: Do ponto de vista pedagógico, o processo acima é excelente para mostrar o significado do MMC mas existe um método prático para realizar tal tarefa sem trabalhar com conjuntos.
Num papel faça um traço vertical, de forma que sobre espaço livre tanto à direita como à esquerda do traço.
Do lado esquerdo do traço escreva os números naturais a, b, c, ... como uma lista, separados por vírgulas, para obter o MMC(a,b,c,...). Por exemplo, tomaremos 12, 22 e 28 do lado esquerdo do traço vertical e do lado direito do traço colocamos o menor número primo que divide algum dos números da lista que está à esquerda.

Dividimos todos os números da lista da esquerda, que são múltiplos do número primo que está à direita do traço, criando uma nova lista debaixo da lista anterior com os valores resultantes das divisões (possíveis) e com os números que não foram divididos.

Repetimos a partir do passo 3 até que os valores da lista que está do lado esquerdo do traço se tornem todos iguais a um.

O MMC é o produto de todos os números primos que colocamos do lado direito do traço.
Neste caso: MMC(12,22,28)=924.
Exemplo: Determinaremos os MMC dos números 12 e 15.
Montagem da tabela:
12 15 | 2
|
|
|
Dividimos todos os números da lista da esquerda pelos números primos (quando a divisão for possível), criando novas listas sob as listas anteriores.
12 15 | 2
6 15 | 2
3 15 | 3
1 5 | 5
1 1 | 60
O MMC(12,15) = 60 é o produto de todos os números primos que colocamos do lado direito do traço.
Máximo Divisor Comum
Para obter o Máximo Divisor Comum devemos introduzir o conceito de divisor comum a vários números naturais. Um número d é divisor comum de outros dois números naturais a e b se, d divide a e d divide b simultaneamente. Assim:
a = k1 x d
e
b = k2 x d
Exemplos: Divisores comuns.
8 é divisor comum de 24 e 56, pois:
24 = 3 x 8 e 56 = 7 x 8
3 é divisor comum de 15 e 36, pois:
15 = 5 x 3 e 36 = 12 x 3
Observação: Um número d é divisor de todos os seus múltiplos. O conjunto dos divisores comuns de dois números é finito, pois o conjunto dos divisores de um número é finito.
Agora determinaremos os divisores comuns aos números 16 e 24.
D(16) = { 1, 2, 4, 8, 16 }
D(24) = { 1, 2, 3, 4, 6, 8, 12, 24 }
D(16)D(24) = {1, 2, 4, 8}
Ocorre que o menor divisor comum entre os números 16 e 24, é 1, assim não interessa o menor divisor comum mas sim o maior divisor que pertence simultaneamente aos dois conjuntos de divisores.
Denotaremos por MDC(a,b), o Máximo Divisor Comum entre os números naturais a e b.
Exemplos: Como:
D(16) = { 1, 2, 4, 8, 16 }
D(24) = {1,2,3,4,6,8,12,24}
então:
MDC(16,24) = max( D(16)D(24)) = 8
Método prático para a determinação do MDC: De forma similar ao cálculo do MMC(a,b), temos também um procedimento prático para determinar o MDC(a,b) entre dois números naturais, pois encontrar conjuntos de divisores para cada número pode ser trabalhoso. Para introduzir este método, determinaremos o MDC entre os números 30 e 72.
Comece construindo uma grade com 3 linhas e algumas colunas, colocando os números dados na linha do meio. Na primeira coluna coloque o maior deles e na segunda coluna o menor.
72 30
Efetue a divisão do maior pelo menor colocando o quociente no espaço sobre o número menor na primeira linha e o resto da divisão no espaço logo abaixo do maior número na terceira linha.
2
72 30
12
Passe o resto da divisão para o espaço localizado à direita do menor número na linha central.
2
72 30 12
12
Realizamos agora a divisão do número 30, pelo resto obtido anteriormente que é 12.
Novamente, o quociente será colocado sobre o número 12 e o resto da divisão ficará localizado abaixo do número 30.
2 2
72 30 12 6
12 6
Realizamos agora a (última!) divisão do número 12, pelo resto obtido anteriormente que é 6.
Novamente, o quociente será colocado sobre o número 6 e o resto da divisão ficará localizado abaixo do número 12.
2 2 2
72 30 12 6
12 6 0
Como o resto da última divisão é 0 (zero), o último quociente encontrado representa o MDC entre 30 e 72, logo denotamos tal fato por:
MDC(30,72)=6
Exercício: Se a diferença entre dois números é 126 e o máximo divisor comum entre eles é 18, quais são esses números?
Solução: Sejam X e Y os tais números procurados. Assim, X e Y devem ser múltiplos de 18, logo podem ser escritos na forma:
X = 18a e Y = 18b
Assim:
18a - 18b = 126
18 (a - b) = 18 × 7
a - b = 7
Tomando a=8 e b=1 teremos X = 144 e Y = 18
Exercício: Se a soma de dois números é 420 e o máximo divisor comum entre eles é 60, quais são esses números?
Solução: Sejam X e Y os tais números procurados. Assim, X e Y devem ser múltiplos de 60, logo podem ser escritos na forma:
X = 60a e Y = 60b
Assim:
60a + 60b = 420
60 (a + b) = 60 × 7
a + b = 7
Tomando a = 6 e b = 1 teremos X = 360 e Y = 60
Exercício: Se a divisão entre dois números é igual a 1,2 e o máximo divisor comum entre eles é 15, quais são esses números?
Solução: Sejam X e Y os tais números procurados. Assim, X e Y devem ser múltiplos de 15, logo podem ser escritos na forma:
X = 15a e Y = 15b
Assim:
15a ÷ 15b = 1,2
a ÷ b = 1,2 = 12 ÷ 10 = 6 ÷ 5
Tomando a = 6 e b = 5, teremos X = 90 e Y = 75
Relação entre o MMC e MDC
Uma relação importante e bastante útil entre o MMC e o MDC é o fato que o MDC(a,b) multiplicado pelo MMC(a,b) é igual ao produto de a por b, isto é:
MDC(a,b).MMC(a,b) = a.b
MDC(12,15).MMC(12,15) = 12.15=180
Exemplo:
MDC(12,15) = 3
MMC(12,15) = 60
3 x 60 = 180 = 12 x 15
Esta relação é útil quando precisamos encontrar o MMC e o MDC de dois números, basta encontrar um deles e usar a relação acima.
Exemplo: Determinar o MMC e o MDC entre 15 e 20.
O primeiro passo é determinar o MDC ou o MMC entre 15 e 20, obtido o MDC(15,20) = 5 e sabendo que 15 x 20 = 300, basta lembrar que MDC(15,20) . MMC(15,20) = 15 x 20 e fazer

Donde obtém-se que o MMC(15,20) é igual a 300 dividido por 5, ou seja MMC(15,20) = 60
Exercício: Se a soma de dois números é 320 e o mínimo múltiplo comum entre eles é 600, quais são esses números? Qual é o máximo divisor comum entre eles?
Solução: Sejam X e Y os números procurados. Assim, X e Y devem satisfazer à relação:
X e Y devem dividir 600, logo devem pertencer ao conjunto
D={1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, 75, 100,
120, 150, 200, 300, 600}
Dois números deste conjunto que somados dão 320, são:
300 e 20 ou 200 e 120
Descartamos o par: 300 e 20 pois mmc(300,20)=300
Os números são X=200 e Y=120 cujo mmc(200,120)=600
O mdc(200,120) = 40.
Primos entre si
Dois números naturais são primos entre si quando o MDC entre eles é igual a um.
Exemplo: 16 não é um número primo, 21 também não é um número primo mas 16 e 21 são primos entre si pois MDC(16,21) = 1
Radiciação de números naturais
Radiciação de ordem n é o processo pelo qual dado um número natural a devemos determinar um número natural b tal que:
bn = a
onde n é um número natural. É o processo inverso da potenciação.
Representamos a operação de radiciação por: Rn[a], a(1/n), pot(a,1/n), pow(a,1/n) ou por um símbolo clássico:

que se lê: raiz n-ésima de a. Uma notação simples e muito comum no meio científico é aquela que usa o acento circunflexo: a^(1/n).
Raiz quadrada: A raiz quadrada de um número não negativo (não somente natural) é um outro número não negativo b tal que:
b2 = a
A raiz quadrada de um número não negativo a pode ser denotada por a^(1/2).
Exemplo: Para determinar a raiz quadrada de 36 deve-se obter b de forma que
b2 = b . b = 36
Por tentativa devemos dividir 36 por seus divisores até que o divisor seja igual ao quociente
36 / 2 = 18
36 / 3 = 12
36 / 4 = 9
36 / 6 = 6
Portanto +6 é a raiz quadrada de 36.
Raiz cúbica: A raiz cúbica de um número (não somente natural) a é um número b tal que:
b3 = b . b . b = a
A raiz cúbica de um número a pode ser denotada por a^(1/3).
Exemplo: Para determinar a raiz cúbica de 64, deve-se determinar b de forma a obter
b3 = b . b . b = 64
Por tentativa, temos :
1 x 1 x 1 = 1
2 x 2 x 2 = 8
3 x 3 x 3 = 27
4 x 4 x 4 = 64
Portanto 4 é raiz cúbica de 64.