SAIBA MAIS:
Um ano luz equivale a cerca de 9,6 trilhões de quilômetros.
Como comparação, o diâmetro da Via Láctea é de aproximadamente 100 mil anos luz.
sábado, 19 de setembro de 2009
NÚMEROS COMPLEXOS
1. Definições
Vimos na resolução de uma equação do 2º grau que se o discriminante é negativo, ela não admite raízes reais.
Por exemplo, a equação x² + 9 = 0não admite raízes reais. Se usarmos os métodos que conhecemos para resolvê-la, obtemos x² = -9x = ± -9 mas é inaceitável tal resultado para x; os números negativos não têm raiz quadrada.
Para superar tal impossibilidade e poder, então, resolver todas equações do 2º grau, os matemáticos ampliaram o sistema de números, inventando os números complexos.Primeiro, eles definiram um novo número i = -1 Isso conduz a i² = -1. Um número complexo é então um número da forma a + bi onde a e b são números reais.
Para a equação acima fazemos x = ± x = ± x = ± . x = ± 3 i As raízes da equação x² + 9 = 0 são 3i e - 3i.
Definição: Um número complexo é uma expressão da forma a + bi onde a e b são números reais e i² = -1. No número complexo a + bi, a é a parte real e b é a parte imaginária.Exemplos 2 + 5i parte real 2 parte imaginária 5 i parte real parte imaginária 12i parte real 0 parte imaginária 12-9 parte real -9 parte imaginária 0. Um número como 12i, com parte real 0, chama-se número imaginário puro. Um número real como -9, pode ser considerado como um número complexo com parte imaginária 0.
Um número complexo por exemplo x² +25 =o temos:
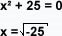
Multimplicamos o valor do discriminante por -1 e obteremos raiz positiva, como -1 é=
i², fica x= +- Raiz de 25i² tirando da raiz obtemos +- 5i
Os números complexos são escritos na sua forma algébrica da seguinte forma: a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo.
Podemos então dizer que um número complexo z será igual a a + bi (z = a + bi).
Com esses números podemos efetuar as operações de adição, subtração e multiplicação, obedecendo à ordem e características da parte real e parte imaginária.
Adição
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao adicionarmos teremos:
z1 + z2
(a + bi) + (c + di)
a + bi + c + di
a + c + bi + di
a + c + (b + d)i
(a + c) + (b + d)i
Portanto, z1 + z2 = (a + c) + (b + d)i.
Exemplo:
Dado dois números complexos z1 = 6 + 5i e z2 = 2 – i, calcule a sua soma:
(6 + 5i) + (2 – i)
6 + 5i + 2 – i
6 + 2 + 5i – i
8 + (5 – 1)i
8 + 4i
Portanto, z1 + z2 = 8 + 4i.
Subtração
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao subtraímos teremos:
z1 - z2
(a + bi) - (c + di)
a + bi – c – di
a – c + bi – di
(a – c) + (b – d)i
Portanto, z1 - z2 = (a - c) + (b - d)i.
Exemplo:
Dado dois números complexos z1 = 4 + 5i e z2 = -1 + 3i, calcule a sua subtração:
(4 + 5i) – (-1 + 3i)
4 + 5i + 1 – 3i
4 + 1 + 5i – 3i
5 + (5 – 3)i
5 + 2i
Portanto, z1 - z2 = 5 + 2i.
Multiplicação
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao multiplicarmos teremos:
z1 . z2
(a + bi) . (c + di)
ac + adi + bci + bdi2
ac + adi + bci + bd (-1)
ac + adi + bci – bd
ac - bd + adi + bci
(ac - bd) + (ad + bc)i
Portanto, z1 . z2 = (ac + bd) + (ad + bc)I.
Exemplo:
Dado dois números complexos z1 = 5 + i e z2 = 2 - i, calcule a sua multiplicação:
(5 + i) . (2 - i)
5 . 2 – 5i + 2i – i2
10 – 5i + 2i + 1
10 + 1 – 5i + 2i
11 – 3i
Portanto, z1 . z2 = 11 – 3i.
Ao dividirmos dois números complexos devemos escrevê-los em forma de fração e multiplicarmos o numerador e o denominador pelo conjugado do denominador, veja como:
Dado dois números complexos z1 e z2, para efetuarmos a divisão dos dois devemos seguir a seguinte regra:
z1 : z2 = z1 .
z2
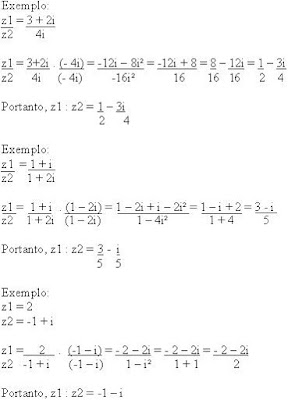.jpg)
De uma forma geral podemos demonstrar a divisão de dois números complexos por:
Dado z1 = a + bi e z2 = c + di a divisão de z1 : z2 será:
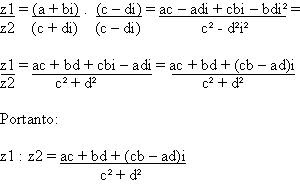.jpg)
Os números complexos são identificados por z = a + bi, onde a é a parte real e b a parte imaginária. A letra i acompanha a parte imaginária e dependo do valor de sua potência ela irá assumir um valor que irá facilitar vários cálculos.
i 0 = 1, pois todo número ou letra elevando à zero é um.
i 1 = i, pois todo número elevado a 1 é ele mesmo.
i 2 = -1, a partir dessa potência que as outras irão derivar, veja:
i 3 = i2 . i = -1 . i = - i
i 4 = i2 . i2 = -1 . (-1) = 1
i 5 = i4 . i = 1 . i = i
i 6 = i4 . i2 = 1 . (-1) = -1.
i 7 = i4 . i3 = 1 . (-i) = - i. E assim por diante.
Para descobrir, por exemplo, qual era o valor da potência i243, basta observar o seguinte: nas potências acima elas repetem-se de 4 em 4, então basta dividirmos 243 por 4, o resto será 3 então i243 será o mesmo que i3, portanto i243 = - i.
Podemos concluir que in = ir, onde r é o resto da divisão.
Vimos na resolução de uma equação do 2º grau que se o discriminante é negativo, ela não admite raízes reais.
Por exemplo, a equação x² + 9 = 0não admite raízes reais. Se usarmos os métodos que conhecemos para resolvê-la, obtemos x² = -9x = ± -9 mas é inaceitável tal resultado para x; os números negativos não têm raiz quadrada.
Para superar tal impossibilidade e poder, então, resolver todas equações do 2º grau, os matemáticos ampliaram o sistema de números, inventando os números complexos.Primeiro, eles definiram um novo número i = -1 Isso conduz a i² = -1. Um número complexo é então um número da forma a + bi onde a e b são números reais.
Para a equação acima fazemos x = ± x = ± x = ± . x = ± 3 i As raízes da equação x² + 9 = 0 são 3i e - 3i.
Definição: Um número complexo é uma expressão da forma a + bi onde a e b são números reais e i² = -1. No número complexo a + bi, a é a parte real e b é a parte imaginária.Exemplos 2 + 5i parte real 2 parte imaginária 5 i parte real parte imaginária 12i parte real 0 parte imaginária 12-9 parte real -9 parte imaginária 0. Um número como 12i, com parte real 0, chama-se número imaginário puro. Um número real como -9, pode ser considerado como um número complexo com parte imaginária 0.
Um número complexo por exemplo x² +25 =o temos:
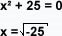
Multimplicamos o valor do discriminante por -1 e obteremos raiz positiva, como -1 é=
i², fica x= +- Raiz de 25i² tirando da raiz obtemos +- 5i
Os números complexos são escritos na sua forma algébrica da seguinte forma: a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo.
Podemos então dizer que um número complexo z será igual a a + bi (z = a + bi).
Com esses números podemos efetuar as operações de adição, subtração e multiplicação, obedecendo à ordem e características da parte real e parte imaginária.
Adição
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao adicionarmos teremos:
z1 + z2
(a + bi) + (c + di)
a + bi + c + di
a + c + bi + di
a + c + (b + d)i
(a + c) + (b + d)i
Portanto, z1 + z2 = (a + c) + (b + d)i.
Exemplo:
Dado dois números complexos z1 = 6 + 5i e z2 = 2 – i, calcule a sua soma:
(6 + 5i) + (2 – i)
6 + 5i + 2 – i
6 + 2 + 5i – i
8 + (5 – 1)i
8 + 4i
Portanto, z1 + z2 = 8 + 4i.
Subtração
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao subtraímos teremos:
z1 - z2
(a + bi) - (c + di)
a + bi – c – di
a – c + bi – di
(a – c) + (b – d)i
Portanto, z1 - z2 = (a - c) + (b - d)i.
Exemplo:
Dado dois números complexos z1 = 4 + 5i e z2 = -1 + 3i, calcule a sua subtração:
(4 + 5i) – (-1 + 3i)
4 + 5i + 1 – 3i
4 + 1 + 5i – 3i
5 + (5 – 3)i
5 + 2i
Portanto, z1 - z2 = 5 + 2i.
Multiplicação
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao multiplicarmos teremos:
z1 . z2
(a + bi) . (c + di)
ac + adi + bci + bdi2
ac + adi + bci + bd (-1)
ac + adi + bci – bd
ac - bd + adi + bci
(ac - bd) + (ad + bc)i
Portanto, z1 . z2 = (ac + bd) + (ad + bc)I.
Exemplo:
Dado dois números complexos z1 = 5 + i e z2 = 2 - i, calcule a sua multiplicação:
(5 + i) . (2 - i)
5 . 2 – 5i + 2i – i2
10 – 5i + 2i + 1
10 + 1 – 5i + 2i
11 – 3i
Portanto, z1 . z2 = 11 – 3i.
Ao dividirmos dois números complexos devemos escrevê-los em forma de fração e multiplicarmos o numerador e o denominador pelo conjugado do denominador, veja como:
Dado dois números complexos z1 e z2, para efetuarmos a divisão dos dois devemos seguir a seguinte regra:
z1 : z2 = z1 .
z2
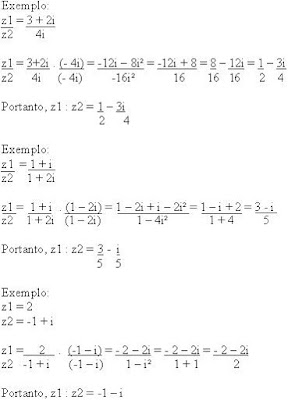.jpg)
De uma forma geral podemos demonstrar a divisão de dois números complexos por:
Dado z1 = a + bi e z2 = c + di a divisão de z1 : z2 será:
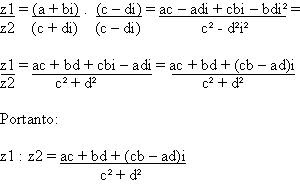.jpg)
Os números complexos são identificados por z = a + bi, onde a é a parte real e b a parte imaginária. A letra i acompanha a parte imaginária e dependo do valor de sua potência ela irá assumir um valor que irá facilitar vários cálculos.
i 0 = 1, pois todo número ou letra elevando à zero é um.
i 1 = i, pois todo número elevado a 1 é ele mesmo.
i 2 = -1, a partir dessa potência que as outras irão derivar, veja:
i 3 = i2 . i = -1 . i = - i
i 4 = i2 . i2 = -1 . (-1) = 1
i 5 = i4 . i = 1 . i = i
i 6 = i4 . i2 = 1 . (-1) = -1.
i 7 = i4 . i3 = 1 . (-i) = - i. E assim por diante.
Para descobrir, por exemplo, qual era o valor da potência i243, basta observar o seguinte: nas potências acima elas repetem-se de 4 em 4, então basta dividirmos 243 por 4, o resto será 3 então i243 será o mesmo que i3, portanto i243 = - i.
Podemos concluir que in = ir, onde r é o resto da divisão.
quarta-feira, 9 de setembro de 2009
CONCEITOS DE GEOMETRIA
Geometria
A necessidade de medir terras determinou os primeiros passos da geometria. O filósofo grego Eudemo de Rodes, do século IV a.C., um dos primeiros historiadores das ciências, conta que os egípcios mediam suas terras para acompanhar o regime de inundações anuais do rio Nilo. De fato, o termo provém das palavras gregas geo (terra) e metron (medida).
No sentido moderno, geometria é a disciplina matemática que tem por objetivo o estudo do espaço e das formas nele contidas.
Aspectos históricos
Nas antigas culturas do Egito e da Mesopotâmia, a geometria consistia simplesmente de um conjunto de regras empíricas. Os gregos, entre os quais destacou-se Euclides, no século III a.C., sistematizaram todos os conhecimentos existentes sobre o tema e estabeleceram seus fundamentos num conjunto de axiomas dos quais, segundo princípios dedutivos, se obtinham os demais resultados. A discussão dos princípios da geometria euclidiana levou à construção, no século XIX, de novos sistemas geométricos, denominados geometrias não-euclidianas, e desembocou na generalização de seus métodos e sua aplicação a espaços cada vez mais abstratos.
Elementos e figuras geométricas
A geometria, em qualquer de suas abordagens, apresenta uma série de elementos primários comuns. Distinguem-se nesse nível os conceitos de plano, ponto, linha (reta, curva etc.), superfície, segmento e outros que, combinados, formam todas as figuras geométricas. As geometrias descritiva e projetiva clássicas se ocupam da representação e das propriedades das figuras e de suas projeções. Distinguem-se nelas algumas figuras geométricas fundamentais.
Polígonos. Um polígono de n lados (sendo n maior ou igual a três) está definido por n pontos ordenados de um plano (A1, A2, ... An) chamados vértices, entre os quais não pode haver três colineares consecutivos. Os n segmentos (A1A2, A2A3, ... AnA1) são chamados lados, e sua interseção forma os vértices.
Polígono é uma linha fechada, isto é, divide o plano em duas regiões, uma interior e outra exterior ao polígono. A diferença entre elas é que qualquer semi-reta cuja origem seja um ponto na região interior corta pelo menos um lado do polígono, o que não acontece necessariamente se o ponto estiver na região exterior. Em função do número de lados (ou ângulos), os polígonos classificam-se em triângulos, quadriláteros, pentágonos, hexágonos, heptágonos, octógonos, eneágonos, decágonos etc.
Triângulos
Os polígonos de três lados recebem o nome de triângulos. Podem ser eqüiláteros (quando os três lados são iguais, ou seja, têm o mesmo comprimento), isósceles (dois lados iguais) ou escalenos (três lados desiguais). De acordo com a medida de seus ângulos, os triângulos dividem-se em acutângulos (se todos os ângulos são menores que 90o), retângulos (se um dos ângulos é reto, ou seja, igual a 90°) e obtusângulos (se um de seus ângulos é maior que 90°). Os três ângulos de um triângulo somam sempre 180°.
Dois triângulos são semelhantes quando os comprimentos dos lados de um deles são respectivamente proporcionais aos lados do outro. Para isso, a condição necessária e suficiente é que os dois triângulos tenham os três ângulos respectivamente iguais. Na verdade, como a soma dos ângulos é sempre 180°, basta que um dos triângulos tenha dois ângulos respectivamente iguais a dois ângulos do outro triângulo para serem semelhantes.
A propriedade da semelhança permite demonstrar várias leis referentes aos triângulos retângulos. Considere-se o triângulo ABC. Os triângulos ABC, ABP e ACP -- onde AP é a altura da hipotenusa (lado oposto ao ângulo reto) - são semelhantes por terem os ângulos iguais. Conseqüentemente, seus lados são proporcionais.
Daí se inferem dois importantes teoremas: um cateto (lado que não é a hipotenusa) é a média proporcional entre a hipotenusa e a projeção dele sobre esta (teorema do cateto, de Euclides); e a altura da hipotenusa é a média proporcional entre as duas partes em que divide esta última (teorema da altura, de Euclides). Ao aplicar-se repetidamente o teorema do cateto, deduz-se o teorema fundamental de Pitágoras: a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Segundo outra demonstração do teorema, a área dos quatro triângulos retângulos é igual à área do quadrado de lado a menos a área do quadrado de lado c~- b:
A perpendicular a cada um dos lados de um triângulo que passa pelo vértice oposto chama-se altura. As três alturas de um triângulo passam por um mesmo ponto, denominado ortocentro. Bissetriz é o segmento, contido no triângulo, que divide o ângulo interno em dois ângulos iguais. O ponto de interseção das bissetrizes dos três ângulos chama-se incentro, por ser o centro da circunferência inscrita no triângulo.
As medianas, ou segmentos que unem cada vértice com o ponto mediano do lado oposto, cortam-se no baricentro, ou centro de gravidade do triângulo. Finalmente, as mediatrizes dos lados (perpendiculares que passam pelo ponto mediano de cada lado) cortam-se no circuncentro, ou centro da circunferência circunscrita ao triângulo. Esses pontos se representam graficamente como mostra a figura.
Para calcular a área de um triângulo, multiplica-se a metade de um de seus lados pela altura correspondente a esse lado. Se são conhecidos os comprimentos dos três lados, a, b e c, pode-se calcular a área pela fórmula de Heron:
onde p é o semiperímetro do triângulo, ou seja, a metade da soma dos comprimentos dos três lados.
Quadriláteros e Polígonos Regulares
Chama-se quadrilátero todo polígono de quatro lados. Os quadriláteros classificam-se em paralelogramos, trapézios e trapezóides, segundo tenham respectivamente dois, um ou nenhum par de lados paralelos. Os paralelogramos podem ser quadrados, retângulos, losangos (ou rombos) e rombóides. Se os ângulos entre os lados forem retos, os paralelogramos serão chamados quadrados e retângulos. Se não forem, serão chamados losangos e rombóides. Os quadrados e losangos têm os quatro lados iguais. Nos retângulos e rombóides os lados são iguais dois a dois.
Para determinar a área, ou superfície (S), de um paralelogramo, multiplica-se a base (qualquer lado) pela altura (distância entre lados paralelos). A área do losango também pode ser determinada como a metade do produto de suas diagonais (diagonal é o segmento de reta que une dois vértices não consecutivos).
Os trapézios podem ser isósceles, quando os dois lados não paralelos são iguais, escalenos, quando são desiguais, e retângulos, quando têm dois ângulos retos. A área de um trapézio é a metade da soma de suas bases (lados paralelos) multiplicada pela altura (distância entre as bases).
Um polígono é regular se todos os seus ângulos, assim como seus lados, forem iguais. Os polígonos regulares se caracterizam pelo fato de poderem ser inscritos ou circunscritos a uma circunferência. A perpendicular a qualquer de seus lados que passa pelo centro do polígono (e que coincide com o raio da circunferência inscrita) chama-se apótema. Ao multiplicar o apótema pela metade do perímetro (soma de todos os lados), obtém-se a área do polígono.
Circunferência
Chama-se circunferência toda curva plana e fechada cujos pontos são eqüidistantes de um ponto interior chamado centro. A porção do plano que está no interior de uma circunferência denomina-se círculo. Os segmentos que unem o centro com qualquer ponto da circunferência chamam-se raios, e os que unem dois pontos quaisquer da circunferência, cordas. As cordas de maior comprimento, que são as que passam pelo centro, são chamadas diâmetros, cada um deles resultante também da união de dois raios em linha reta.
O comprimento linear de uma circunferência é igual a duas vezes o seu raio, multiplicado por um número irracional denominado , que vale 3,14159... Nos cálculos, costuma-se deixá-lo indicado sem substituir por seu valor aproximado. A área do círculo é o produto do número pelo quadrado do raio.
O cálculo de - que é o quociente entre o comprimento linear de uma circunferência qualquer e seu diâmetro - se faz a partir da sucessão de perímetros de polígonos regulares (de três, quatro, cinco, seis etc. lados), inscritos e circunscritos em circunferências de raio igual a 1. As duas sucessões de perímetros (a dos polígonos inscritos e a dos circunscritos) têm como limite o número , que seria o perímetro de um polígono com um número tão grande de lados que coincidiria com uma circunferência. Arquimedes demonstrou que o valor de estava compreendido entre .
Por meio de computadores e séries de potências, já foi possível calcular cem mil casas decimais de . Para as quinze primeiras casas temos igual a 3,141592653589793... O número é irracional, por não ter dízimas periódicas, e transcendente, por não ser solução de nenhuma equação algébrica com coeficientes inteiros.
A porção de círculo compreendida entre um arco e dois raios chama-se setor circular, e a limitada por um arco e uma corda, segmento circular. Calculam-se as áreas dessas superfícies por meio das fórmulas que se seguem à figura.
Poliedros
Os sólidos limitados por polígonos planos denominam-se poliedros, que são chamados regulares quando suas faces são polígonos regulares iguais. Há cinco tipos de poliedros regulares: com faces triangulares (o tetraedro, com quatro faces; o octaedro, com oito; e o icosaedro, com vinte); com faces quadradas (o cubo, ou hexaedro, com seis faces); e com faces pentagonais (o dodecaedro, com 12 faces).
Denomina-se superfície poliédrica aquela formada por um número finito de polígonos ou faces, e que satisfaz duas condições: (1) cada lado de uma face pertence também a uma outra face, e só a uma, contígua; (2) duas faces contíguas não pertencem a um mesmo plano.
Uma superfície com essas características é fechada, uma vez que é demarcada pelos polígonos e permite distinguir entre pontos interiores e exteriores a ela. Poliedro é o conjunto dos pontos interiores a uma superfície poliédrica. Os pontos comuns a três ou mais faces (e portanto a três ou mais lados dos polígonos que compõem as faces) chamam-se vértices. Cada lado de polígono, comum ao polígono de uma face contígua, chama-se aresta.
Chama-se prisma todo poliedro que tem duas faces iguais e paralelas de n lados (bases) e n faces laterais em forma de paralelogramo. Se as faces laterais forem perpendiculares às bases, os prismas são chamados retos; caso contrário, chamam-se oblíquos. Se as bases de um prisma são paralelogramos, esse prisma é um paralelepípedo.
Se o poliedro é formado por um polígono de n lados (base) e n faces triangulares com um vértice comum, chama-se pirâmide. O ponto comum é o vértice da pirâmide, e sua distância até a base, a altura. Se a pirâmide for cortada por um plano paralelo à base, obtêm-se dois poliedros: uma outra pirâmide, menor, e um tronco de pirâmide. As duas faces paralelas do tronco de pirâmide são polígonos semelhantes de n lados, e as n faces laterais são trapezoidais.
Esfera, cilindro e cone. Toda superfície fechada formada por pontos eqüidistantes de um ponto interior chamado centro é uma superfície esférica. Essa figura geométrica também pode ser definida como a superfície gerada por uma circunferência que gira tendo um de seus diâmetros como eixo. Esfera é o conjunto dos pontos de uma superfície esférica e dos pontos interiores a ela. A interseção de uma esfera com um plano forma um círculo, que será máximo se o plano passar pelo centro da esfera, e tanto menor quanto mais distante passar do centro.
Cilindro é um corpo gerado por um retângulo que gira, tendo um de seus lados como eixo. O cilindro é demarcado por duas bases circulares e uma superfície lateral.
Se um triângulo retângulo gira tendo como eixo um de seus catetos, ele gera um cone, que é demarcado por duas superfícies apenas: a base circular e a superfície lateral
A necessidade de medir terras determinou os primeiros passos da geometria. O filósofo grego Eudemo de Rodes, do século IV a.C., um dos primeiros historiadores das ciências, conta que os egípcios mediam suas terras para acompanhar o regime de inundações anuais do rio Nilo. De fato, o termo provém das palavras gregas geo (terra) e metron (medida).
No sentido moderno, geometria é a disciplina matemática que tem por objetivo o estudo do espaço e das formas nele contidas.
Aspectos históricos
Nas antigas culturas do Egito e da Mesopotâmia, a geometria consistia simplesmente de um conjunto de regras empíricas. Os gregos, entre os quais destacou-se Euclides, no século III a.C., sistematizaram todos os conhecimentos existentes sobre o tema e estabeleceram seus fundamentos num conjunto de axiomas dos quais, segundo princípios dedutivos, se obtinham os demais resultados. A discussão dos princípios da geometria euclidiana levou à construção, no século XIX, de novos sistemas geométricos, denominados geometrias não-euclidianas, e desembocou na generalização de seus métodos e sua aplicação a espaços cada vez mais abstratos.
Elementos e figuras geométricas
A geometria, em qualquer de suas abordagens, apresenta uma série de elementos primários comuns. Distinguem-se nesse nível os conceitos de plano, ponto, linha (reta, curva etc.), superfície, segmento e outros que, combinados, formam todas as figuras geométricas. As geometrias descritiva e projetiva clássicas se ocupam da representação e das propriedades das figuras e de suas projeções. Distinguem-se nelas algumas figuras geométricas fundamentais.
Polígonos. Um polígono de n lados (sendo n maior ou igual a três) está definido por n pontos ordenados de um plano (A1, A2, ... An) chamados vértices, entre os quais não pode haver três colineares consecutivos. Os n segmentos (A1A2, A2A3, ... AnA1) são chamados lados, e sua interseção forma os vértices.
Polígono é uma linha fechada, isto é, divide o plano em duas regiões, uma interior e outra exterior ao polígono. A diferença entre elas é que qualquer semi-reta cuja origem seja um ponto na região interior corta pelo menos um lado do polígono, o que não acontece necessariamente se o ponto estiver na região exterior. Em função do número de lados (ou ângulos), os polígonos classificam-se em triângulos, quadriláteros, pentágonos, hexágonos, heptágonos, octógonos, eneágonos, decágonos etc.
Triângulos
Os polígonos de três lados recebem o nome de triângulos. Podem ser eqüiláteros (quando os três lados são iguais, ou seja, têm o mesmo comprimento), isósceles (dois lados iguais) ou escalenos (três lados desiguais). De acordo com a medida de seus ângulos, os triângulos dividem-se em acutângulos (se todos os ângulos são menores que 90o), retângulos (se um dos ângulos é reto, ou seja, igual a 90°) e obtusângulos (se um de seus ângulos é maior que 90°). Os três ângulos de um triângulo somam sempre 180°.
Dois triângulos são semelhantes quando os comprimentos dos lados de um deles são respectivamente proporcionais aos lados do outro. Para isso, a condição necessária e suficiente é que os dois triângulos tenham os três ângulos respectivamente iguais. Na verdade, como a soma dos ângulos é sempre 180°, basta que um dos triângulos tenha dois ângulos respectivamente iguais a dois ângulos do outro triângulo para serem semelhantes.
A propriedade da semelhança permite demonstrar várias leis referentes aos triângulos retângulos. Considere-se o triângulo ABC. Os triângulos ABC, ABP e ACP -- onde AP é a altura da hipotenusa (lado oposto ao ângulo reto) - são semelhantes por terem os ângulos iguais. Conseqüentemente, seus lados são proporcionais.
Daí se inferem dois importantes teoremas: um cateto (lado que não é a hipotenusa) é a média proporcional entre a hipotenusa e a projeção dele sobre esta (teorema do cateto, de Euclides); e a altura da hipotenusa é a média proporcional entre as duas partes em que divide esta última (teorema da altura, de Euclides). Ao aplicar-se repetidamente o teorema do cateto, deduz-se o teorema fundamental de Pitágoras: a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Segundo outra demonstração do teorema, a área dos quatro triângulos retângulos é igual à área do quadrado de lado a menos a área do quadrado de lado c~- b:
A perpendicular a cada um dos lados de um triângulo que passa pelo vértice oposto chama-se altura. As três alturas de um triângulo passam por um mesmo ponto, denominado ortocentro. Bissetriz é o segmento, contido no triângulo, que divide o ângulo interno em dois ângulos iguais. O ponto de interseção das bissetrizes dos três ângulos chama-se incentro, por ser o centro da circunferência inscrita no triângulo.
As medianas, ou segmentos que unem cada vértice com o ponto mediano do lado oposto, cortam-se no baricentro, ou centro de gravidade do triângulo. Finalmente, as mediatrizes dos lados (perpendiculares que passam pelo ponto mediano de cada lado) cortam-se no circuncentro, ou centro da circunferência circunscrita ao triângulo. Esses pontos se representam graficamente como mostra a figura.
Para calcular a área de um triângulo, multiplica-se a metade de um de seus lados pela altura correspondente a esse lado. Se são conhecidos os comprimentos dos três lados, a, b e c, pode-se calcular a área pela fórmula de Heron:
onde p é o semiperímetro do triângulo, ou seja, a metade da soma dos comprimentos dos três lados.
Quadriláteros e Polígonos Regulares
Chama-se quadrilátero todo polígono de quatro lados. Os quadriláteros classificam-se em paralelogramos, trapézios e trapezóides, segundo tenham respectivamente dois, um ou nenhum par de lados paralelos. Os paralelogramos podem ser quadrados, retângulos, losangos (ou rombos) e rombóides. Se os ângulos entre os lados forem retos, os paralelogramos serão chamados quadrados e retângulos. Se não forem, serão chamados losangos e rombóides. Os quadrados e losangos têm os quatro lados iguais. Nos retângulos e rombóides os lados são iguais dois a dois.
Para determinar a área, ou superfície (S), de um paralelogramo, multiplica-se a base (qualquer lado) pela altura (distância entre lados paralelos). A área do losango também pode ser determinada como a metade do produto de suas diagonais (diagonal é o segmento de reta que une dois vértices não consecutivos).
Os trapézios podem ser isósceles, quando os dois lados não paralelos são iguais, escalenos, quando são desiguais, e retângulos, quando têm dois ângulos retos. A área de um trapézio é a metade da soma de suas bases (lados paralelos) multiplicada pela altura (distância entre as bases).
Um polígono é regular se todos os seus ângulos, assim como seus lados, forem iguais. Os polígonos regulares se caracterizam pelo fato de poderem ser inscritos ou circunscritos a uma circunferência. A perpendicular a qualquer de seus lados que passa pelo centro do polígono (e que coincide com o raio da circunferência inscrita) chama-se apótema. Ao multiplicar o apótema pela metade do perímetro (soma de todos os lados), obtém-se a área do polígono.
Circunferência
Chama-se circunferência toda curva plana e fechada cujos pontos são eqüidistantes de um ponto interior chamado centro. A porção do plano que está no interior de uma circunferência denomina-se círculo. Os segmentos que unem o centro com qualquer ponto da circunferência chamam-se raios, e os que unem dois pontos quaisquer da circunferência, cordas. As cordas de maior comprimento, que são as que passam pelo centro, são chamadas diâmetros, cada um deles resultante também da união de dois raios em linha reta.
O comprimento linear de uma circunferência é igual a duas vezes o seu raio, multiplicado por um número irracional denominado , que vale 3,14159... Nos cálculos, costuma-se deixá-lo indicado sem substituir por seu valor aproximado. A área do círculo é o produto do número pelo quadrado do raio.
O cálculo de - que é o quociente entre o comprimento linear de uma circunferência qualquer e seu diâmetro - se faz a partir da sucessão de perímetros de polígonos regulares (de três, quatro, cinco, seis etc. lados), inscritos e circunscritos em circunferências de raio igual a 1. As duas sucessões de perímetros (a dos polígonos inscritos e a dos circunscritos) têm como limite o número , que seria o perímetro de um polígono com um número tão grande de lados que coincidiria com uma circunferência. Arquimedes demonstrou que o valor de estava compreendido entre .
Por meio de computadores e séries de potências, já foi possível calcular cem mil casas decimais de . Para as quinze primeiras casas temos igual a 3,141592653589793... O número é irracional, por não ter dízimas periódicas, e transcendente, por não ser solução de nenhuma equação algébrica com coeficientes inteiros.
A porção de círculo compreendida entre um arco e dois raios chama-se setor circular, e a limitada por um arco e uma corda, segmento circular. Calculam-se as áreas dessas superfícies por meio das fórmulas que se seguem à figura.
Poliedros
Os sólidos limitados por polígonos planos denominam-se poliedros, que são chamados regulares quando suas faces são polígonos regulares iguais. Há cinco tipos de poliedros regulares: com faces triangulares (o tetraedro, com quatro faces; o octaedro, com oito; e o icosaedro, com vinte); com faces quadradas (o cubo, ou hexaedro, com seis faces); e com faces pentagonais (o dodecaedro, com 12 faces).
Denomina-se superfície poliédrica aquela formada por um número finito de polígonos ou faces, e que satisfaz duas condições: (1) cada lado de uma face pertence também a uma outra face, e só a uma, contígua; (2) duas faces contíguas não pertencem a um mesmo plano.
Uma superfície com essas características é fechada, uma vez que é demarcada pelos polígonos e permite distinguir entre pontos interiores e exteriores a ela. Poliedro é o conjunto dos pontos interiores a uma superfície poliédrica. Os pontos comuns a três ou mais faces (e portanto a três ou mais lados dos polígonos que compõem as faces) chamam-se vértices. Cada lado de polígono, comum ao polígono de uma face contígua, chama-se aresta.
Chama-se prisma todo poliedro que tem duas faces iguais e paralelas de n lados (bases) e n faces laterais em forma de paralelogramo. Se as faces laterais forem perpendiculares às bases, os prismas são chamados retos; caso contrário, chamam-se oblíquos. Se as bases de um prisma são paralelogramos, esse prisma é um paralelepípedo.
Se o poliedro é formado por um polígono de n lados (base) e n faces triangulares com um vértice comum, chama-se pirâmide. O ponto comum é o vértice da pirâmide, e sua distância até a base, a altura. Se a pirâmide for cortada por um plano paralelo à base, obtêm-se dois poliedros: uma outra pirâmide, menor, e um tronco de pirâmide. As duas faces paralelas do tronco de pirâmide são polígonos semelhantes de n lados, e as n faces laterais são trapezoidais.
Esfera, cilindro e cone. Toda superfície fechada formada por pontos eqüidistantes de um ponto interior chamado centro é uma superfície esférica. Essa figura geométrica também pode ser definida como a superfície gerada por uma circunferência que gira tendo um de seus diâmetros como eixo. Esfera é o conjunto dos pontos de uma superfície esférica e dos pontos interiores a ela. A interseção de uma esfera com um plano forma um círculo, que será máximo se o plano passar pelo centro da esfera, e tanto menor quanto mais distante passar do centro.
Cilindro é um corpo gerado por um retângulo que gira, tendo um de seus lados como eixo. O cilindro é demarcado por duas bases circulares e uma superfície lateral.
Se um triângulo retângulo gira tendo como eixo um de seus catetos, ele gera um cone, que é demarcado por duas superfícies apenas: a base circular e a superfície lateral
Assinar:
Postagens (Atom)