Assunto: Ensinando matemática

 
A Evolução da Educação...
Antigamente se ensinava e cobrava tabuada, caligrafia, redação, datilografia...
Havia aulas de Educação Física, Moral e Cívica, Práticas Agrícolas, Práticas Industriais e cantava-se o Hino Nacional, hasteando a Bandeira Nacional antes de iniciar as aulas.
Leiam relato de uma Professora de Matemática:
Semana passada, comprei um produto que custou R$15,80. Dei à balconista R$ 20,00 e peguei na minha bolsa 80 centavos, para evitar receber ainda mais moedas. A balconista pegou o dinheiro e ficou olhando para a máquina registradora, aparentemente sem saber o que fazer. Tentei explicar que ela tinha que me dar R$5,00 reais de troco, mas ela não se convenceu e chamou o gerente para ajudá-la. Ficou com lágrimas nos olhos enquanto o gerente tentava explicar e ela aparentemente continuava sem entender. Por que estou contando isso?
Porque me dei conta da evolução do ensino de matemática desde 1950, que foi assim:

1. Ensino de matemática em 1950:
Um lenhador vende um carro de lenha por R$ 100,00. O custo de
produção é igual a 4/5 do preço de venda. Qual é o lucro?
2. Ensino de matemática em 1970:
Um lenhador vende um carro de lenha por R$ 100,00. O custo de produção é igual a 4/5 do preço de venda ou R$ 80,00. Qual é o lucro?
3. Ensino de matemática em 1980:
Um lenhador vende um carro de lenha por R$ 100,00. O custo de
produção é R$ 80,00. Qual é o lucro?
4. Ensino de matemática em 1990:
Um lenhador vende um carro de lenha por R$ 100,00. O custo de produção é R$ 80,00. Escolha a resposta certa, que indica o lucro:
a) ( )R$ 20,00
b) ( )R$ 40,00
c) ( )R$ 60,00
d) ( )R$ 80,00
e) ( )R$ 100,00
5. Ensino de matemática em 2000:
Um lenhador vende um carro de lenha por R$ 100,00. O custo de
produção é R$ 80,00. O lucro é de R$ 20,00.
Está certo?
a) ( )SIM
b) ( ) NÃO
6. Ensino de matemática em 2009:
Um lenhador vende um carro de lenha por R$ 100,00. O custo de produção é R$ 80,00. Se você souber ler coloque um X no R$ 20,00.
a) ( )R$ 20,00
b) ( )R$ 40,00
c) ( )R$ 60,00
d) ( )R$ 80,00
e) ( )R$ 100,00
7. Em 2011 vai ser assim:
Um lenhador vende um carro de lenha por R$ 100,00. O custo de produção é R$ 80,00. Se você souber ler coloque um X no R$ 20,00. (Se você é afro descendente, especial, indígena ou de qualquer outra minoria social não precisa responder)
a) ( )R$ 20,00
b) ( )R$ 40,00
c) ( )R$ 60,00
d) ( )R$ 80,00
e) ( )R$ 100,00
PS. Ainda existe a possibilidade da professora ser advertida, por ter feito uma questão muito difícil de ser respondida.

Geometria Espacial » cilindros

 

Geometria Espacial

 

 

áreas e volumes

Função quadrática

 

Estratégias e recursos da aula

O trabalho com funções é desafiador para alunos e professores. São necessárias operações variadas, produção e análise de gráficos e também o estudo de suas aplicações. O objetivo dessa aula é criar condições para que o aluno trabalhe com a função quadrática e atinja um nível de entendimento adequado. Para isso usaremos um objeto de aprendizagem que apresenta uma aplicação prática e mostraremos como podem ser criados gráficos dessa importante função.

   

TIPOS DE FRAÇÕES

 

Tipos de Frações:

.

Frações Próprias: São aquelas onde o numerador é menor que o denominador. . Frações Impróprias: São aquelas onde o numerador é maior que o denominador.   . É a fração que representa as duas figuras acima juntas, note que no numerador houve a soma das partes coloridas , já o denominador foi repetido, pois cada imagem possuí oito partes iguais. . Frações Aparentes: São aquelas em que o numerador é múltiplo do denominador. . É a fração que representa as duas figuras acima juntas, note que no numerador houve a soma das partes coloridas das imagens, já o denominador foi repetido, pois cada imagem possuí seis partes iguais. Esta fração é aparente pois 12 (numerador) é múltiplo de 6 (denominador). . Números Mistos: Frações aparentes também podem ser frações impróprias, sendo representadas de uma forma especifica, os chamados números mistos. . É a fração que representa as duas figuras acima juntas, note que no numerador houve a soma das partes coloridas das imagens, já o denominador foi repetido, pois cada imagem possuí seis partes iguais. . Esta fração também pode ser representada da seguinte forma, ou seja, um inteiro e dois sextos, sendo este um número misto. . Logo: . Para Transformar um Número Misto em Fração Imprópria basta seguir o exemplo abaixo: Repete o denominador e multiplica o seu valor com a parte inteira e soma com o numerador.

DICA PARA RECONHECIMENTO DOS NÚMEROS PRIMOS

Diz a Matemática que não se sabe como calcular números primos: são números sem divisores, apenas divisíveis por si mesmo e pela unidade. Uma das questões matemáticas mais antigas, pendente de esclarecimento, é a de que números primos não têm um padrão - são caóticos e não existe um processo matemático para determiná-los com precisão na linha dos números.

Apesar de complexos, existem modos para determinar a primariedade, para saber se um número é ou não é primo, mas não existe uma fórmula matemática para criá-los. O processo ainda hoje utilizado para identificar números primos é o chamado Crivo de Erastótenes (Matemático grego – 276/194 a.C), pelo qual vai se excluindo os números que têm divisores até restarem apenas os primos. Muitos matemáticos têm buscado resolver a questão dos números primos, e alguns deles dedicaram parte de sua vida a isso, mas os resultados têm sido parciais. Em 2002, dois indianos anunciaram um algoritmo para, através do computador, encontrar números primos, mas o processo, mesmo assim, ainda é bastante complexo. Enfim, em tese, primos são números caóticos. É com base nesse fato que a criptografia se apoia para esconder informação e criar senhas na informática. A descoberta de uma solução para números primos significaria, aparentemente, um abalo na segurança criptográfica computacional, mas a ciência não pode parar.

Para se saber se um número natural ou primo é ou não, divide-se esse número pelos sucessivos números primos: 2, 3, 5, 7, 11, 13,17, 19... até obter-se um quociente exato (se não for primo) ou um quociente igual ou menor que o divisor se for primo)

Exemplos:

· O número 157 é primo?

157 78 157 : 3 = 52 157 : 5 = 31 157 : 7 = 22 157 : 11 = 14

157: 13 = 12

Solução: O número 157 é primo, pois o (12) DA ÚLTIMA DIVISÃO é menor que o divisor (13) e nenhuma das DIVISÕES foi exata.

· O número 161 é primo?

161 : 2 = 80 161 : 3 = 53 161 : 5 = 32 161 : 7 = 23

Solução: O número 161 não é primo, pois a última divisão é exata

Teorema de Tales

 

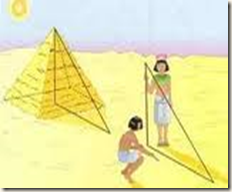
Tales de Mileto foi um importante filósofo, astrônomo e matemático grego que viveu antes de Cristo. Ele usou seus conhecimentos sobre Geometria e proporcionalidade para determinar a altura de uma pirâmide. Em seus estudos, Tales observou que os raios solares que chegavam à Terra estavam na posição inclinada e eram paralelos, dessa forma, ele concluiu que havia uma proporcionalidade entre as medidas da sombra e da altura dos objetos, observe a ilustração:

Com base nesse esquema, Tales conseguiu medir a altura de uma pirâmide com base no tamanho da sua sombra. Para tal situação ele procedeu da seguinte forma: fincou uma estaca na areia, mediu as sombras respectivas da pirâmide e da estaca em uma determinada hora do dia e estabeleceu a proporção:

O Teorema de Tales pode ser determinado pela seguinte lei de correspondência:
“Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes”.
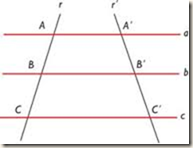
Para compreender melhor o teorema observe o esquema representativo a seguir:

Pela proporcionalidade existente no Teorema, temos a seguinte situação:

Exemplo 1
Aplicando a proporcionalidade existente no Teorema de Tales, determine o valor dos segmentos AB e BC na ilustração a seguir:

AB = 2x – 3
BC = x + 2
A’B’ = 5
B’C’ = 6
Determinando o valor de x:

AB = 2x – 3 → 2*4 – 3 = 5
BC = x + 2 → 4 + 2 = 6
Exemplo 2
Determine o valor de x na figura a seguir:

Teorema de Tales

 

 

Três paralelas cortadas por duas transversais, formando quatro segmentos. Essa imagem como do desenho acima é representação mais clássica do Teorema de Tales.

LEMBRANÇAS DE EX-ALUNOS

 

        

 

O NÚMERO QUE VOCÊ CALÇA

 

• A matemática e o número que você calça

Relação entre o número que você calça e o tamanho de seu pé.

Muitas vezes não entendemos os motivos de se estudar matemática ou quando vamos usar determinada parte do conteúdo e, por isso, nos questionamos: onde a matemática é realmente aplicada?

Inúmeros são os exemplos e situações onde podemos ver o emprego da matemática. Desde o momento em que acordamos até a hora de dormir, estamos sempre fazendo o uso dessa ciência. Quando, ao levantar pela manhã para ir à escola ou fazer qualquer atividade, dizemos “só mais cinco minutinhos”, intuitivamente estamos realizando cálculos matemáticos para averiguar se esses preciosos minutos de sono não ocasionarão um atraso. A tecnologia não estaria tão avançada sem o fantástico auxílio da matemática. Do mais simples ato até a mais sofisticada empregabilidade, a matemática está sempre presente em nosso cotidiano, basta que analisemos as situações que vivenciamos.

Por mais inimaginável que possa parecer, o número que você calça também está relacionado à matemática. Existe uma fórmula que relaciona o número que você calça e o tamanho do seu pé em centímetros.

Vejamos:

Onde,

S: é o número do sapato.
p: é o comprimento do pé em centímetros.

Assim, se seu pé medir 20 cm, o número do seu sapato será:

Dividindo em Partes Iguais

 

 

• Dividindo em Partes Iguais

Frações

Frações

Joana e sua mãe foram à pizzaria. Elas pediram uma pizza de calabresa tamanho médio. A pizza foi dividida ao meio, isto é, em duas partes iguais.

Representamos essa situação utilizando frações. Cada parte é chamada de metade da pizza. Podemos mostrar isso pela fração da metade da pizza:

Um meio

Podemos dividir a pizza em quantas partes forem necessárias, dependendo do número de pessoas.
Dividindo a pizza em três partes iguais

Cada pedaço recebe o nome de terça parte, e é representada por:

Um terço

Dividindo a pizza em quatro partes iguais

Agora, cada pedaço recebe o nome de quarta parte, e é representado por:

Um quarto
Vamos imaginar que Joana e mais sete amigas foram à pizzaria. Pediram uma pizza grande, a qual seria dividida em 8 partes iguais. Veja:

Cada pedaço é denominado por oitava parte, e a representação será através da seguinte fração:

Um oitavo.