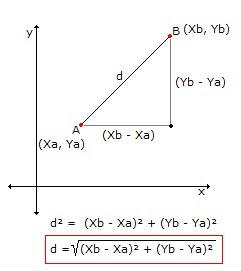quinta-feira, 26 de março de 2009
quinta-feira, 19 de março de 2009
EXERCÍCIOS DE FIXAÇÃO RELAÇÕES MÉTRICAS
conteúdo desenvolvido dia 20 de março de 2009
DISCIPLINA MATEMÁTICA
INSTRUMENTO DE FIXAÇÃO DO CONTEÚDO RELAÇÕES MÉTRICA

1.) No triângulo retângulo ABC da figura, calcule:
a.) h, para m = 9 e n = 4 cm
b.) a, para m = 3 cm e n= 9 cm
c.) a, para b = 8 cm e c = 6 cm
d.) b, para a = 13 cm e c = 6 cm
e.) h, sendo b = 3 cm e c = 4 cm
1. No triângulo retângulo ABC da figura, calcule:
a) A medida dos catetos b e c (b = 20 cm e c =15 cm)
b) A medida da altura h
c) A medida do cateto c (b = 3 hipotenusa = 5)
3.) Calcule quando mede:
a) A hipotenusa de um triângulo retângulo de catetos 3cm e 4cm.
b) Um dos catetos de um triângulo retângulo em que a hipotenusa mede 4 cm e outro cateto mede 3 cm.
quarta-feira, 18 de março de 2009
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
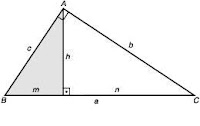
a: hipotenusa
b e c: catetos
h: altura relativa a hipotenusa
m e n: projeções ortogonais dos catetos sobre a hipotenusa.
Relações métricas
Para um triângulo retângulo ABC podemos estabelecer algumas relações entre as medidas de seus elementos:
- O quadrado de um cateto é igual ao produto da hipotenusa pela projeção desse cateto sobre a hipotenusa.
b² = a.n c² = a.m
- O produto dos catetos é igual ao produto da hipotenusa pela altura relativa a hipotenusa.
b.c = a.h
- O quadrado da altura é igual ao produto das projeções dos catetos sobre a hipotenusa.
h² = m.n
- O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
a² = b² + c²
Essa relação é conhecida pelo nome de TEOREMA DE PITÁGORAS.
Exemplo:
Neste triângulo ABC, vamos calcular a, h, m e n:
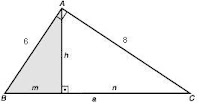
a² = b² + c² → a² = 6² + 8² → a² = 100 → a = 10
b.c = a.h → 8.6 = 10.h → h = 48/10 = 4,8
c² = a.m → 6² = 10.m → m = 36/10 = 3,6
b² = a.n → 8² = 10.n → n = 64/10 = 6,4
Determine os valores literais indicados nas figuras:
a)

13² = 12² + x² 5.12 = 13.y
169 = 144 + x² y = 60/13
x² = 25
x = 5
b)

c)

d)

Determine a altura de um triângulo eqüilátero de lado l.

Determine x nas figuras.
a)

O triângulo ABC é eqüilátero.
b)

c)

Determine a diagonal de um quadrado de lado l.

Razões trigonométricas
Considere um triângulo retângulo ABC. Podemos definir:
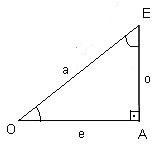
- Seno do ângulo agudo: razão entre o cateto oposto ao ângulo e a hipotenusa do triângulo.
senÊ = e/a senÔ = o/a
- Cosseno do ângulo agudo: razão entre o cateto adjacente ao ângulo e a hipotenusa do triângulo.
cosÊ = o/a cosÔ = e/a
- Tangente do ângulo agudo: razão entre o cateto oposto ao ângulo e o cateto adjacente.
tgÊ = e/o tgÔ = o/e
Observe: senÊ = cosÔ, senÔ = cosÊ e tgÊ = 1/tgÔ, sempre Ê + Ô = 90º
Exemplo:

senÔ = 3/5 = 0,6 senÊ = 4/5 = 0,8
cosÔ = 4/5 = 0,8 cosÊ = 3/5 = 0,6
tgÔ = 3/4 = 0,75 tgÊ = 4/3 = 1,333....
Ângulos notáveis
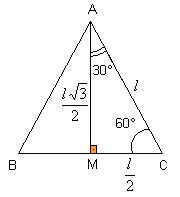
Podemos determinar seno, cosseno e tangente de alguns ângulos. Esses ângulos chamados de notáveis, são: 30°, 45° e 60°. A partir das definições de seno, cosseno e tangente, vamos determinar esses valores para os ângulos notáveis. Considere um triângulo eqüilátero de lado l. Traçando a altura AM, obtemos o triângulo retângulo AMC de ângulos agudos iguais a 30° e 60°. Aplicando as razões trigonométricas ao triângulo AMC temos:
Para obter as razões trigonométricas do ângulo de 45°, considere um quadrado de lado l. A diagonal divide o quadrado em dois triângulos retângulos isósceles.
No triângulo ABD, temos:
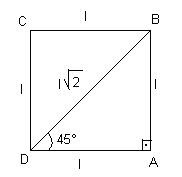
Observação: sen45° = cos45°
Resumindo temos a tabela:

Exercícios resolvidos:
1) Calcule o perímetro do triângulo retângulo ABC da figura, sabendo que o segmento BC é igual a 10 m e cos α = 3/5

sexta-feira, 13 de março de 2009
CIRCUNFERÊNCIA CONTEÚDO EM DESENVOLVIMENTO NA SALA DE AULA

.............................................................
Circunferência
Seja um ponto qualquer do plano e um número real. A circunferência de centro e raio é o lugar geométrico dos pontos desse plano tais que .
Arco de circunferência
Consideremos uma circunferência de centro . Sejam e dois pontos distintos de .
Um arco de circunferência de extremos e é cada uma das partes em que fica dividida uma circunferência por dois de seus pontos.
Quando teremos dois arcos: o arco nulo (um ponto) e o arco de uma volta (uma circunferência).


Arco de circunferência e ângulo central correspondente
A medida de um arco é, por definição, a medida do ângulo central correspondente. Medir significa comparar com uma unidade padrão previamente adotada. Contudo, para evitar possíveis divergências na escolha da unidade para medir um mesmo arco, as unidades de medida restringem-se a três principais: o grau (), o radiano () e o grado, sendo este último não muito comum.

O grau
Um grau é um arco de circunferência cujo comprimento equivale a da circunferência que contém o arco a ser medido. Portanto, a medida, em graus, de um arco de uma volta completa (uma circunferência) é .

Submúltiplos do grau
O minuto : , ou seja, .
O segundo : , ou seja, e .
O radiano
Um radiano é um arco de circunferência cujo comprimento é igual ao raio da circunferência que contém o arco a ser medido. É a unidade do Sistema Internacional (SI).
Conseqüentemente, para medir um ângulo em radianos, convém calcular a razão entre o comprimento do arco pelo raio , ou seja, calcular quantos radianos mede o arco . Portanto, como consequência da definição de radiano, podemos estabelecer a seguinte relação:
, onde e devem estar na mesma unidade de comprimento.
O comprimento de uma circunferência de raio é . Logo, a medida do arco de uma volta completa, em radianos, é . Para converter unidades, podemos usar as correspondências ou e uma regra de três simples.
O grado
É a medida de um arco cujo comprimento equivale a da circunferência que contém o arco a ser medido. É evidente que, para conversão de unidades, pode-se utilizar as relações ou e uma regra de três simples.
O ciclo trigonométrico
Consideremos no plano um sistema de eixos perpendiculares , em que . Seja uma circunferência de centro , raio e o ponto .

A cada número real associaremos um único ponto de .
Se , então tomamos ;
Se , realizamos, a partir de , um percurso de comprimento , no sentido anti-horário e marcamos o ponto como final desse percurso.
Se , realizamos, a partir de ,um percurso de comprimento , no sentido horário, e marcamos o ponto como final desse percurso.
.

Assim, a circunferência sobre a qual foi fixado o ponto como orientação é chamada ciclo trigonométrico ou circunferência trigonométrica
O ponto é chamado imagem de no ciclo trigonométrico.
O sistema de eixos perpendiculares divide o ciclo trigonométrico em quatro partes, cada uma das quais é chamada quadrante.
Ângulos côngruos
Os ângulos e , em graus, são côngruos ou congruentes se, e somente se, , para algum , ou seja, se e têm a mesma imagem no ciclo trigonométrico. Para indicar que e são côngruos escrevemos .
Por exemplo, os ângulos e são congruentes, pois .
Expressão geral dos arcos que têm imagem em um ponto do ciclo trigonométrico..
Consideremos um sistema de eixos perpendiculares e uma circunferência de centro e raio . Sendo um ponto qualquer pertencente à a imagem de um ângulo na circunferência, podemos estabelecer uma expressão geral dos arcos que têm imagem em um determinado ponto do ciclo trigonométrico.
Por exemplo, a expressão geral dos arcos que têm imagem no ponto dar-se-á por ou , sendo o número de voltas completas. Quando , deve-se andar no sentido anti-horário; se , deve-se andar no sentido horário.
Analogamente, temos:
Para : ou .
Para : ou .
Para : ou .
Para ou : ou .
Para ou : ou .
Para ou ou ou : ou .
Considerando a figura acima, a expressão geral dos arcos que têm imagem em ou é:
em graus:
em radianos:
Expressão geral dos arcos que têm imagem em :
em graus:
em radianos:
No caso da figura seguinte, a expressão geral dos arcos fica:
em graus:
em radianos:
Imagens de alguns arcos importantes
Primeira volta no sentido anti-horário:
Ângulos correspondentes
Em graus:
Em radianos:
quarta-feira, 11 de março de 2009
ÁLGEBRA I - conjuntos


Turmas 11
Este conteúdo esta sendo desenvolvido com as turmas 12, 13, e 13A
Unidade 1
Álgebra (I)
1. Conjuntos e conjuntos numéricos
2. Funções
3. Função afim
4. Função quadrática
5. Função modular
6. Função exponencial
7. Logaritmo e função logarítmica
8. Progressões
l. CONJUNTOS E CONJUNTOS NUMÉRICOS
Analise a seguinte situação-problema:

Em uma pesquisa realizada com 50 pessoas para saber que esporte elas apreciam entre futebol, basquete e vôlei, o resultado foi o seguinte: 23 gostam de futebol, 18 gostam de basquete e 14 gostam de vôlei; 10 gostam de futebol e de basquete; 9 de futebol e de vôlei; 8 de basquete e de vôlei; e 5 gostam das três modalidades.
a) Quantas pessoas não gostam de nenhum desses esportes?
b) Quantas gostam somente de futebol?
c) Quantas gostam só de basquete?
d) Quantas gostam apenas de vôlei?
e) E quantas não gostam nem de basquete nem de vôlei?
f) Quantas pessoas gostam só de futebol ou só de basquete ou de ambas?
(Para resolver questões desse tipo, devemos utilizar conhecimentos de conjuntos)
2 A noção de conjunto
A noção de conjunto é bastante simples e fundamental na Matemática, pois a partir dela podem ser expressas os conceitos matemáticos.
Um conjunto é uma coleção qualquer de objetos. Por exemplo:
• Conjunto dos estados da região Sudeste do Brasil:
S = {São Paulo, Rio de Janeiro, Minas Gerais, Espírito Santo}
• Conjunto dos números primos
B = {2, 3, 5, 7, 11, 13...}
Um conjunto é formado por elemento.

Um objeto a qualquer pode ser elemento de um determinado conjunto A.
Quanto for, dizemos que:
a pertence a A e escrevemos a ∊ A
GEOMETRIA ANALÍTICA
TURMAS 34 e 35 (noturno)
Aula dada para turma 34 e 35
dia 10 de março de 2009
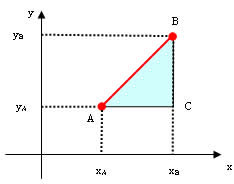
Distância entre dois pontos
Se soubermos as coordenadas de dois pontos no plano cartesiano (ponto A e B), é possível determinar a sua distância, utilizando o teorema de Pitágoras
(a² = b² + c²)
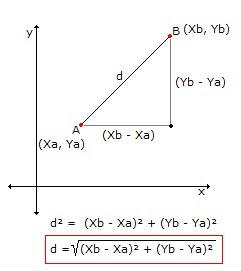
Exemplo:
Calcule a distancia entre os pontos dados A (3,l) B(4,6)

Exercícios propostos em sala de aula (Livro didático Dante, Luiz Roberto 3a. série
página 10, 11 exercícios 8, 9, 10, 11, 12, 13, 14, 15, 15, 17, 18, 19)
aula data 20 de março de 2009.
EXERCÍCIOS SOBRE DISTÂNCIA ENTRE DOIS PONTOS
1. Calcule a distância entre os pontos dados:
a) A (3, 7) e B(1, 4)
b) E (3, -1) e F (3, 5)
c) H (-2, -5)e O (0, 0)
2. A distância do ponto A(a, 1) ao ponto b 0, 2) é igual a 3. Calcule o valor da abscissa a.
3. Um ponto P pertence ao eixo das abscissas e é eqüidistante dos pontos A(-1,2) e B (1 , 4) Quais s]ao as coordenadas do ponto P?
SOLUÇÃO:
l.
a) d(A,B) = V13
b) d(A,B) = 6
c) d(A,B) = V29
2. Se d (A,B) = 3 então a2 =8 => a = ± 2 √2
3.Se P pertence ao eixo das abscissas, então suas coordenadas são a e 0.
Como P (a,0) é equidistante de A e B, devemos ter d(P,A) = d(P,B). Assim:
a=3
Logo, o ponto P é (3,0) e as coordenadas do ponto P são 3 e 0.
quarta-feira, 4 de março de 2009
GEOMETRIA ANALITICA
DIA 02 DE MARÇO DE 2009
.......................................................................
.

1 - Introdução
A Geometria Analítica é uma parte da Matemática , que através de processos particulares , estabelece as relações existentes entre a Álgebra e a Geometria. Desse modo , uma reta , uma circunferência ou uma figura podem ter suas propriedades estudadas através de métodos algébricos .
Os estudos iniciais da Geometria Analítica se deram no século XVII , e devem-se ao filósofo e matemático francês René Descartes (1596 - 1650), inventor das coordenadas cartesianas (assim chamadas em sua homenagem), que permitiram a representação numérica de propriedades geométricas. No seu livro Discurso sobre o Método, escrito em 1637, aparece a célebre frase em latim "Cogito ergo sum" , ou seja: "Penso, logo existo".
O estudo da geometria é dividido em algumas partes, uma delas é a Geometria Analítica.
A geometria analítica faz a análise detalhada de termos importantes para o estudo da geometria em geral, como analisar a reta, o plano, o ponto.
Essa análise é dividida em tópicos:
• Coordenadas na reta
• Coordenadas no plano
• Segmentos de reta no plano
• A distância entre dois pontos
• Escolhendo o sistema de coordenadas
• Outros tipos de coordenadas
• As equações da reta
• Ângulo entre duas retas
• Distância de um ponto a uma reta
• Área de um triângulo
• Desigualdades lineares
• Equação da circunferência
• Reconhecimento da equação da circunferência
• Vetores no plano
• Operações com vetores
• Equação da elipse
• Equação da hipérbole
• Equação da parábola
• Mudança de coordenadas
• Formas quadráticas
• A equação geral do segundo grau
• O sinal de uma forma quadrática
• As equações paramétricas de uma reta
• Distância entre dois pontos no espaço
• Segmentos de Reta no Espaço
• Vetores no Espaço
• Equação do Plano
1.1 - Coordenadas cartesianas na reta
Seja a reta r na Fig. abaixo e sobre ela tomemos um ponto O chamado origem.
Adotemos uma unidade de medida e suponhamos que os comprimentos medidos a partir de O, sejam positivos à direita e negativos à esquerda.
______A'_________0___________A_______________>
______-1_________0___________+1______________>
O comprimento do segmento OA é igual a 1 u.c (u.c = unidade de comprimento). É fácil concluir que existe uma correspondência um a um (correspondência biunívoca) entre o conjunto dos pontos da reta e o conjunto R dos números reais. Os números são chamados abscissas dos pontos. Assim, a abscissa do ponto A’ é -1, a abscissa da origem O é 0, a abscissa do ponto A é 1, etc.
A reta r é chamada eixo das abscissas.
r_________________u________________
1.2 - Coordenadas cartesianas no plano
Com o modo simples de se representar números numa reta, visto acima, podemos estender a idéia para o plano, basta que para isto consideremos duas retas perpendiculares que se interceptem num ponto O, que será a origem do sistema.

Para começar o estudo da geometria analítica, é necessário conhecer o Plano Cartesiano:
O Eixo Y (linha vertical) é chamado de eixo das ordenadas, enquanto que o Eixo X (linha horizontal), é chamado de eixo das abscissas.
O ponto P (ponto vermelho da figura) possui duas coordenadas: X e Y , que indicam em que lugar dos eixos das ordenadas e abscissas ele se encontra. Representa-se isso por (Xp, Yp).
Os números romanos nos cantos mostram os quadrantes do plano cartesiano. Os pontos do eixo X que estão nos quadrantes II e III são negativos, enquanto que em I e IV são positivos. Os valores de Y nos quadrantes I e II são positivos, e nos restantes (III e IV), esses valores são negativos.
Bissetrizes
As bissetrizes são retas que cortam exatamente o centro do plano cartesiano ( ponto (0, 0) ), e formam um ângulo de 45º com os eixos X e Y. As coordenadas dos pontos que estão sobre a bissetriz que se encontra nos quadrantes pares são sempre opostos (se X for positivo, Y será negativo, e vice-versa).
Já os pontos sobre a bissetriz dos quadrantes ímpares, terão os valores de X e Y iguais. Veja no desenho abaixo:
1.1 - Coordenadas cartesianas no plano
Com o modo simples de se representar números numa reta, visto acima, podemos estender a idéia para o plano, basta que para isto consideremos duas retas perpendiculares que se interceptem num ponto O, que será a origem do sistema. Veja a Fig. a seguir:

Dizemos que a é a abscissa do ponto P e b é a ordenada do ponto P. O eixo OX é denominado eixo das abscissas e o eixo OY é denominado eixo das ordenadas. O ponto O(0,0) é a origem do sistema de coordenadas cartesianas.Os sinais algébricos de a e b definem regiões do plano denominadas QUADRANTES. No 1º quadrante, a e b são positivos, no 2º quadrante, a é negativo e b positivo, no 3º quadrante, ambos são negativos e finalmente no 4º quadrante a é positivo e b negativo.Observe que todos os pontos do eixo OX tem ordenada nula e todos os pontos do eixo OY tem abscissa nula. Assim, dizemos que a equação do eixo OX é y = 0 e a equação do eixo OY é x = 0. Os pontos do plano onde a = b, definem uma reta denominada bissetriz do 1º quadrante, cuja equação evidentemente é y = x. Já os pontos do plano onde a = -b (ou b = - a), ou seja, de coordenadas simétricas, definem uma reta denominada bissetriz do 2º quadrante, cuja equação evidentemente é y = - x. Os eixos OX e OY são denominados eixos coordenados.
Exercícios Resolvidos
EXERCÍCIOS SOBRE DISTÂNCIA ENTRE DOIS PONTOS
1. Calcule a distância entre os pontos dados:
a) A (3, 7) e B(1, 4)
b) E (3, -1) e F (3, 5)
c) H (-2, -5)e O (0, 0)
2. A distância do ponto A(a, 1) ao ponto b 0, 2) é igual a 3. Calcule o valor da abscissa a.
3. Um ponto P pertence ao eixo das abscissas e é eqüidistante dos pontos A(-1,2) e B (1 , 4) Quais s]ao as coordenadas do ponto P?
SOLUÇÃO:
l.
a) d(A,B) = V13
b) d(A,B) = 6
c) d(A,B) = V29
2. Se d (A,B) = 3 então a2 =8 => a = ± 2 √2
3.Se P pertence ao eixo das abscissas, então suas coordenadas são a e 0.
Como P (a,0) é equidistante de A e B, devemos ter d(P,A) = d(P,B). Assim:
a=3
Logo, o ponto P é (3,0) e as coordenadas do ponto P são 3 e 0.
Distância entre dois pontos
Se soubermos as coordenadas de dois pontos no plano cartesiano (ponto A e B), é possível determinar a sua distância, utilizando o teorema de Pitágoras
(a² = b² + c²)