Vimos na resolução de uma equação do 2º grau que se o discriminante é negativo, ela não admite raízes reais.
Por exemplo, a equação x² + 9 = 0não admite raízes reais. Se usarmos os métodos que conhecemos para resolvê-la, obtemos x² = -9x = ± -9 mas é inaceitável tal resultado para x; os números negativos não têm raiz quadrada.
Para superar tal impossibilidade e poder, então, resolver todas equações do 2º grau, os matemáticos ampliaram o sistema de números, inventando os números complexos.Primeiro, eles definiram um novo número i = -1 Isso conduz a i² = -1. Um número complexo é então um número da forma a + bi onde a e b são números reais.
Para a equação acima fazemos x = ± x = ± x = ± . x = ± 3 i As raízes da equação x² + 9 = 0 são 3i e - 3i.
Definição: Um número complexo é uma expressão da forma a + bi onde a e b são números reais e i² = -1. No número complexo a + bi, a é a parte real e b é a parte imaginária.Exemplos 2 + 5i parte real 2 parte imaginária 5 i parte real parte imaginária 12i parte real 0 parte imaginária 12-9 parte real -9 parte imaginária 0. Um número como 12i, com parte real 0, chama-se número imaginário puro. Um número real como -9, pode ser considerado como um número complexo com parte imaginária 0.
Um número complexo por exemplo x² +25 =o temos:

Multimplicamos o valor do discriminante por -1 e obteremos raiz positiva, como -1 é=
i², fica x= +- Raiz de 25i² tirando da raiz obtemos +- 5i
Os números complexos são escritos na sua forma algébrica da seguinte forma: a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo.
Podemos então dizer que um número complexo z será igual a a + bi (z = a + bi).
Com esses números podemos efetuar as operações de adição, subtração e multiplicação, obedecendo à ordem e características da parte real e parte imaginária.
Adição
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao adicionarmos teremos:
z1 + z2
(a + bi) + (c + di)
a + bi + c + di
a + c + bi + di
a + c + (b + d)i
(a + c) + (b + d)i
Portanto, z1 + z2 = (a + c) + (b + d)i.
Exemplo:
Dado dois números complexos z1 = 6 + 5i e z2 = 2 – i, calcule a sua soma:
(6 + 5i) + (2 – i)
6 + 5i + 2 – i
6 + 2 + 5i – i
8 + (5 – 1)i
8 + 4i
Portanto, z1 + z2 = 8 + 4i.
Subtração
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao subtraímos teremos:
z1 - z2
(a + bi) - (c + di)
a + bi – c – di
a – c + bi – di
(a – c) + (b – d)i
Portanto, z1 - z2 = (a - c) + (b - d)i.
Exemplo:
Dado dois números complexos z1 = 4 + 5i e z2 = -1 + 3i, calcule a sua subtração:
(4 + 5i) – (-1 + 3i)
4 + 5i + 1 – 3i
4 + 1 + 5i – 3i
5 + (5 – 3)i
5 + 2i
Portanto, z1 - z2 = 5 + 2i.
Multiplicação
Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao multiplicarmos teremos:
z1 . z2
(a + bi) . (c + di)
ac + adi + bci + bdi2
ac + adi + bci + bd (-1)
ac + adi + bci – bd
ac - bd + adi + bci
(ac - bd) + (ad + bc)i
Portanto, z1 . z2 = (ac + bd) + (ad + bc)I.
Exemplo:
Dado dois números complexos z1 = 5 + i e z2 = 2 - i, calcule a sua multiplicação:
(5 + i) . (2 - i)
5 . 2 – 5i + 2i – i2
10 – 5i + 2i + 1
10 + 1 – 5i + 2i
11 – 3i
Portanto, z1 . z2 = 11 – 3i.
Ao dividirmos dois números complexos devemos escrevê-los em forma de fração e multiplicarmos o numerador e o denominador pelo conjugado do denominador, veja como:
Dado dois números complexos z1 e z2, para efetuarmos a divisão dos dois devemos seguir a seguinte regra:
z1 : z2 = z1 .
z2
.jpg)
De uma forma geral podemos demonstrar a divisão de dois números complexos por:
Dado z1 = a + bi e z2 = c + di a divisão de z1 : z2 será:
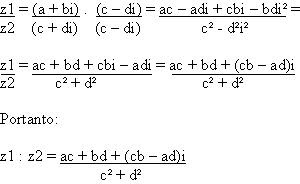.jpg)
Os números complexos são identificados por z = a + bi, onde a é a parte real e b a parte imaginária. A letra i acompanha a parte imaginária e dependo do valor de sua potência ela irá assumir um valor que irá facilitar vários cálculos.
i 0 = 1, pois todo número ou letra elevando à zero é um.
i 1 = i, pois todo número elevado a 1 é ele mesmo.
i 2 = -1, a partir dessa potência que as outras irão derivar, veja:
i 3 = i2 . i = -1 . i = - i
i 4 = i2 . i2 = -1 . (-1) = 1
i 5 = i4 . i = 1 . i = i
i 6 = i4 . i2 = 1 . (-1) = -1.
i 7 = i4 . i3 = 1 . (-i) = - i. E assim por diante.
Para descobrir, por exemplo, qual era o valor da potência i243, basta observar o seguinte: nas potências acima elas repetem-se de 4 em 4, então basta dividirmos 243 por 4, o resto será 3 então i243 será o mesmo que i3, portanto i243 = - i.
Podemos concluir que in = ir, onde r é o resto da divisão.
Nenhum comentário:
Postar um comentário