
Uma matriz recebe certo tipo de nome dependendo da quantidade de elementos em suas linhas e colunas ou apenas por características específicas.
►Matriz linhas
Recebe o nome de Matriz linha toda matriz que possui apenas uma linha. O número de colunas é independente. Por exemplo:
[-5 1 2]1 x 3
►Matriz coluna
Recebe o nome de Matriz coluna toda matriz que possuir apenas uma coluna. O número de linhas é independente. Por exemplo:

►Matriz nula
Recebe o nome de Matriz nula toda matriz que independentemente do número de linhas e colunas todos os seus elementos são iguais a zero. Por exemplo:

Podendo ser representada por 3 x 2.
►Matriz quadrada
Matriz quadrada é toda matriz que o número de colunas é o mesmo do número de linhas. Por exemplo:

Quando a matriz é quadrada nela podemos perceber a presença de uma diagonal secundária e uma diagonal principal.

►Matriz diagonal
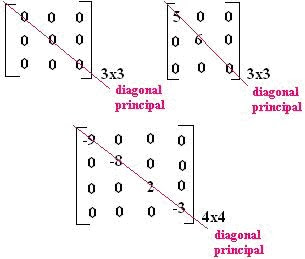
Será uma matriz diagonal, toda matriz quadrada que os elementos que não pertencem à diagonal principal sejam iguais a zero. Sendo que os elementos da diagonal principal podem ser iguais a zero ou não. Por exemplo:
►Matriz identidade
Para que uma matriz seja matriz identidade ela tem que ser quadrada e os elementos que pertencerem à diagonal principal devem ser iguais a 1 e o restante dos elementos iguais a zero. Veja o exemplo:

►Matriz oposta
Dada uma matriz B, a matriz oposta a ela é - B. Se tivermos uma matriz:

A matriz oposta a ela é:

Concluímos que, para encontrar a matriz oposta de uma matriz qualquer basta trocar os sinais dos elementos.
►Matrizes iguais ou igualdade de matrizes
Dada uma matriz A e uma matriz B, as duas poderão ser iguais se somente seus elementos correspondentes forem iguais.

As matrizes A e B são iguais, pois seus elementos correspondentes são iguais
Nenhum comentário:
Postar um comentário