Seja uma circunferência de centro O sobre a qual tomamos dois pontos distintos, A e B. A seguir, ainda sobre a circunferência, tomemos um terceiro ponto M, distinto dos anteriores. A circunferência fica dividida em duas partes, cada uma das quais é um arco de circunfernciâ
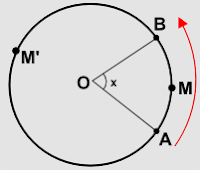
Arco de circunferência AMB, e
Arco de circunferência AM'B.
A e B são as extremidades do arco. É importante lembrar que:
A cada arco tomado corresponde um ângulo central e a medida de um arco equivale à medida do ângulo central correspondente.
Assim , por exemplo, se, na figura, x é a medida do ângulo central AÔB então m(AMB) = x. Analogamente se y é a medida do outro ângulo central então m(AM'B) = y.
Se não houver dúvida quando ao arco a que nos referimos, podemos escrever apenas AB ao invés de AMB.
Atenção: não confunda medida de arco com comprimento de arco. Estes são conceitos bem diferentes. Se por exemplo você puder “cortar” a circunferência mostrada na figura acima nos pontos A e B e em seguida “alinhar” cada um dos dois arcos segundo um segmento de reta e medir o comprimento desses segmentos (com uma régua, por exemplo) você obterá como resultados os comprimentos dos dois arcos.
MEDIDAS DE ARCOS E ÂNGULOS
Medir um arco (ou ângulo) é compará-lo com outro, unitário.
GRAU
Um grau é definido como a medida do ângulo central subtendido por um arco igual a 1/360 da circunferência que contém o arco. (Indica-se 1º). Então podemos dizer que uma circunferência (ou arco de uma volta) mede 360º.
RADIANOS
O radiano (notação: rad) é definido como a medida de um ângulo central subtendido por um arco cujo comprimento é igual ao raio da circunferência que contém o arco. A circunferência toda contém 2π raios, o que significa que seu comprimento é igual a 2πr e que a medida dela (correspondente ao arco de uma volta) é de 2π rad. Na matemática π (letra do alfabeto grego que se lê como pi) representa um número irracional (e também transcendente) que representa o valor do comprimento de uma circunferência dividido pelo seu diâmetro. Matemáticos do Egito antigo descobriram que a razão entre o comprimento de uma circunferência e seu diâmetro é a mesma para qualquer circunferência. Eles definiram esta razão como, o que hoje chamamos de π, "um número um pouco maior que 3". O valor de π com 63 casas decimais depois da vírgula é
3,141.592.653.589.793.238.462.643.383.279.502.884.197.169.
399.375.105.820.974.944.592.
É interessante observar que os egípcios chegaram ao valor aproximado de 3,16 há 3500 anos partindo de um quadrado inscrito numa circunferncia, cujo lado media nove unidades. Eles, então, dobraram os lados do quadrado para obter um polígono de oito lados e calcularam a razão entre os perímetros dos octógonos inscrito e circunscrito e o diâmetro da circunferência.
Quer saber um pouco mais, consulte: http://pt.wikipedia.org/wiki/Pi. )
Sabendo-se que a circunferência (ou arco de uma volta) mede 360° ou 2πrad, podemos estabelecer entre as unidades as relações:
360° <-> 2πrad
180° <-> π rad
O percurso sobre um arco desde sua origem até sua extremidade poderá ser feito em dois sentidos: horário ou anti-horário. Arco AB orientado no
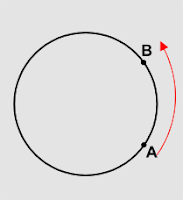
sentido Horário:
Arco AB orientado no
sentido Anti-horário:

Nenhum comentário:
Postar um comentário