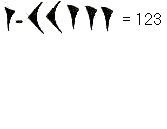PROGRESSÕES ARITMÉTICAS E GEOMÉTRICAS: HISTÓRIA,
CONCEITOS E APLICAÇÕES
FONTE DE PESQUISA
Valéria Scomparim de LIMA (Profª Drª ) – UNIMEP – UNOPEC – FAM
Acácio Reis da Silva – Alexandre Côa
Ariane Carrara – Carla Roberta Furlan
Edi Francisco Grandino – Fernando Spessotto Assarice
Gilson A. Saldibas Alonso – Márcia Cristina Tavares
Nathália Garcia Natal – Patrícia Gomes Pimenta
Paulo Rogério Rizzo – UNIMEPINTRODUÇÃO:
Muitas pessoas pensam que a Matemática é uma disciplina em que só
se trabalha com um grande número de fórmulas sem sentido e com cálculos
intermináveis. Em nossas escolas o ensino das progressões é “passado” aos
alunos, enquanto deveria ser construído junto com eles, nota-se também que
esses conceitos não são abordados a partir da história e não tem ligação com a
realidade dos mesmos.
Mas, o objetivo desse trabalho é mostrar que as coisas não são bem
assim, afinal nós podemos encontrar a matemática em todo o nosso cotidiano,
como as seqüências com que ocorrem alguns fatos como, por exemplo, as
estações do ano, que se repetem obedecendo a um padrão, os números das
placas dos veículos também são exemplos de seqüências ou progressões.
Esse trabalho tem a intenção de, com o apoio de diversas técnicas,
atividades, problemas e inclusive, da parte histórica, ajudar as pessoas a
compreender as progressões. Estudando inicialmente, os processos geniais
que ao longo da história tantos homens encontraram para enfrentar os
problemas do dia-a-dia, tendo em vista o que ela, a história, pode oferecer
como contribuição ao processo de ensino e aprendizagem da Matemática,
verificando que esses conceitos surgiram das necessidades dos antigos povos
babilônicos e egípcios, se estendendo até os dias de hoje.
Num segundo momento, estão dispostos os conceitos, fórmulas e
suas demonstrações, sendo de grande valia ressaltar que elas partem de
pressupostos reais, e que não são inventadas.
Por fim salientamos as aplicações dos conceitos estudados, no
nosso meio, com a utilização de meios tecnológicos. Sendo assim, vamos
mostrar que a Matemática não é abstrata a ponto de não se conseguir aplicar
em nada, uma vez que ela pode e deve estar ao alcance de todos.
HISTÓRIA DAS PROGRESSÕES ARITMÉTICAS E GEOMÉTRICAS
As progressões foram estudadas desde povos muito antigos
como os babilônicos.

Inicialmente, procurou-se
estabelecer padrões como o da
enchente do Rio Nilo, onde os
egípcios de 5.000 anos atrás
tiveram que observar os
períodos em que ocorria a
enchente do rio, pois para
poderem plantar na época certa
e assim garantir seus alimentos, os egípcios precisavam saber quando haveria
inundação. Havia, portanto, necessidade de se conhecer o padrão desse
acontecimento.
Eles observaram que o rio subia logo depois que a estrela Sírius
se levantava a leste, um pouco antes do Sol. Notando que isso acontecia a
cada 365 dias, os egípcios criaram um calendário solar composto de doze
meses, de 30 dias cada mês e

mais cinco dias de festas,dedicados aos deuses Osíris,
Hórus, Seth, Ísis e Nephthys.
Os egípcios dividiram
ainda os doze meses em três
estações de quatro meses cada
uma: período de semear, período
de crescimento e período da colheita.
Rio Nilo
Tableta Babilônica
Na Mesopotâmia surgiram várias tabletas babilônicas muito
interessantes, mas nenhuma delas foi tão extraordinária quanto a tableta
Plimpton 322 (1900 a 1600 a.C.). Numa dessas tabletas, a progressão
geométrica 1+2+2²+...+29 é somada de forma que a série de quadrados
1²+2²+3²+...+10² é achada.
A Matemática no Egito antigo nunca alcançou o nível obtido pela
Matemática babilônica, talvez porque os egípcios tenham se mantido em semi
isolamento, enquanto a babilônia era o centro das rotas de navios, e
consequentemente, era um centro de troca de saberes. No entanto, devemos
lembrar que os egípcios desenvolveram um papel primordial na preservação de
muitos papiros que contribuíram para o nosso conhecimento atual sobre a
Matemática.
Em um papiro que data de 1950 a. C. podemos encontrar alguns
problemas teóricos a respeito de Progressões Aritméticas e Geométricas. Esse
papiro foi encontrado em Kahun e contém o seguinte problema:
“Uma dada

superfície de 100 unidades de
área deve ser representada
como a soma de dois
quadrados cujos lados estão
entre si como 1 : ¾”.
Nesse caso
temos x² + y² = 100 e x = 3y /
4. A eliminação de x fornece
uma equação quadrática em y.
Podemos, porém, resolver o
problema por falsa posição.
Para isso tomemos y = 4.
Então x = 3 e x² + y² = 25 em
vez de 100. Por conseguinte devemos fazer a correção de x e y dobrando os
valores iniciais, o que dá x = 6 e y = 8.
O papiro Rhind (ou Ahmes) data aproximadamente de 1650 a. C.
e nada mais é do que um texto matemático na forma de manual prático que
Papiro Rhind
contém 85 problemas copiados em escrita hierática pelo escriba Ahmes de um
trabalho mais antigo.
Esse papiro foi adquirido no Egito pelo egiptólogo escocês A.
Henry Rhind, sendo mais tarde comprado pelo Museu Britânico. O papiro Rhind
foi publicado em 1927. Tem cerca de dezoito pés de comprimento por cerca de
treze polegadas de altura. Porém, quando o papiro chegou ao Museu Britânico
ele era menor, formado de duas partes, e faltava-lhe a porção central.
Cerca de quatro anos depois de Rhind ter adquirido seu papiro, o
egiptólogo americano Edwin Smith comprou no Egito o que pensou que fosse
um papiro médico. A aquisição de Smith foi doada À Sociedade Histórica de
Nova York em 1932, quando os especialistas descobriram por sob uma
camada fraudulenta a parte que faltava do papiro de Ahmes. A Sociedade,
então, doou o rolo de pergaminho ao Museu Britânico, completando-se assim
todo o trabalho de Ahmes. O papiro Rhind é uma fonte primária rica sobre a
matemática egípcia antiga, deixando evidências de que sabiam fazer a soma
dos termos de uma progressão aritmética.
O seguinte problema envolvendo progressões se encontra no
papiro Rhind:
“Divida 100 pães entre 5 homens de modo que as partes
recebidas estejam em Progressão Aritmética e que um sétimo da soma das
três partes maiores seja igual à soma das duas menores”.
Muitos dos cálculos no Papiro Rhind são evidentemente exercícios para
jovens estudantes. Embora uma grande parte deles seja de natureza prática ,
em algumas ocasiões o escriba parece ter tido em mente enigmas ou
recreações matemáticas. O problema 79, por exemplo, cita apenas “sete casa,
49 gatos, 343 ratos, 2041 espigas de trigo, 16 807 hectares”. É presumível que
o escriba estava tratando de um problema bem conhecido, em que uma das
sete casas havia sete gatos, cada um deles come sete ratos, cada um dos
quais havia comido sete espigas, cada uma delas teria produzido sete medidas
de grão. O problema evidentemente não pedia uma resposta prática, que seria
o numero de medidas de grãos poupadas, mas a não-prática soma dos
números de casas, gatos, ratos, espigas e medidas de grão.
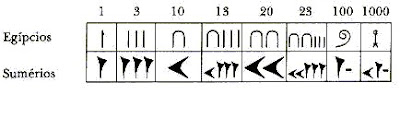
No Papiro de Rhind também aparece uma progressão geométrica muito
interessante formada pelas frações ½, ¼, 1/8, 1/16, 1/32, 1/64 do Hekat,
(unidade comum do volume usada para medir quantidade de grãos). Os termos
dessa seqüência são conhecidos como frações dos olhos do deus Hórus.

Os egípcios estavam aptos a somar progressões geométricas com 6
elementos, usando multiplicação por um fator comum:
Os egipicios multiplicariam todos os elementos por 64 (o ultimo
denominador) e encontrariam:
Então:
Daí:
Os babilônicos também utilizavam seqüências. Foram
encontrados 2 problemas interessantes sobre seqüência numa tábua de
Louvre, datando por volta de 300 a.C. Um deles afirma que:
1+ 2 + 22 + 23 + 24... + 28 + 29 = 29 + 29 −1
64
1
32 elementos por 64 (o ultimo
denominador) e encontrariam:
Então:
Daí:
Os babilônicos também utilizavam seqüências. Foram
encontrados 2 problemas interessantes sobre seqüência numa tábua de
Louvre, datando por volta de 300 a.C. Um deles afirma que:
1+ 2 + 22 + 23 + 24... + 28 + 29 = 29 + 29 −1
64
1
32
1
16
1
8
1
4
1
2
S =
1
16
1
8
1
4
1
2
S = 1 + + + + +
64
64 1
32
64 1
16
64 1
8
64 1
4
64 1
2
64 ⋅ S = 64 ⋅ 1 + ⋅ + ⋅ + ⋅ + ⋅ + ⋅
64
63
64 32 16 8 4 2 1 63
=
⋅ = + + + + + =
S
.

Presume-se que se deve a Pitágoras (585 a.C. –
500 a.C.) e aos sábios gregos que viveram depois dele, a
criação da Aritmética teóricos, pois os pitagóricos conheciam
as progressões aritméticas, as geométricas, as harmônicas e
musicais, as proporções, os quadrados de uma soma ou de
uma diferença
Ele associou o número à música e à mística,
derivando-se dessa associação pitagórica os termos " média harmônica " e "
progressão harmônica ". Como conseqüência de várias observações,
concluíram que a relação entre a altura dos sons e a largura da corda da lira
seria responsável pela existência da harmonia musical. Observaram, também,
que os intervalos musicais se colocam de modo que admite expressão através
de progressões aritméticas.
Pode-se dizer que suas origens remontam à Antigüidade, quando
Pitágoras e seus discípulos fizeram um estudo das cordas vibrantes.
Embora certamente não tenham sido os pitagóricos os primeiros a
observar que a vibração de uma corda tensionada é capaz de produzir variados
sons, a eles se deve a primeira teoria sobre o relacionamento entre a musica e
a matemática.
A importância desses fatos, para Pitágoras, residia em que novos
tons relacionados com o original por meio de frações, isto é, estabeleciam-se
relações entre os números naturais. Confirma-se, pois, ainda mais a sua teoria
de que tudo no Universo estaria relacionado com os números naturais.
Os Números Figurados se originaram através dos membros mais
antigos da escola pitagórica em aproximadamente 600 a. C.. Esses números,
que expressam o número de pontos em certas configurações geométricas,
representam um elo de ligação entre a geometria e a aritmética. Na figura
abaixo se justifica a nomenclatura “números triangulares”:
Evidentemente o enésimo número triangular Tn é dado pela soma
da Progressão Aritmética, lembrando que a soma dos termos de uma
Progressão Aritmética finita é a metade do produto do número de termos pela
soma dos dois termos extremos, temos:
Pitágoras
Tn = 1 + 2 + 3+ ... + n =
2
n.(n +1)
.
Nesta outra figura se justifica a nomenclatura Números
Pentagonais:
O enésimo número pentagonal Pn é também dado pela soma de
uma Progressão Aritmética:
Pn = 1 + 4 + 7 + ... + (3n – 2) =
2
n.(3n −1)
= n +
2
3n.(n −1)
= n + 3 Tn - 1
O grego Euclides de Alexandria também teve grande êxito na
história da matemática, produzindo a obra Os Elementos. A primeira edição
desse trabalho surgiu em 1482 e depois desta data já surgiram mais de mil.
Nenhum trabalho, exceto a Bíblia, foi tão largamente usado ou estudado e,
provavelmente, nenhum exerceu influência maior no pensamento científico,
afinal, por mais de dois milênios esse trabalho dominou o ensino de geometria.
Os Elementos se compõem de 465 proposições distribuídas em
treze livros, e é no livro VIII que encontramos as proporções contínuas e
Progressões Geométricas relacionadas, de forma que, se temos uma
proporção contínua a : b = b : c = c : d, então a, b, c, d formam uma Progressão
Geométrica.
O problema 21 do livro IV diz: “Encontre três números em
Progressão Geométrica de maneira que a diferença entre dois quaisquer deles
é um quadrado”. Segundo o autor do problema a resposta é 81/7, 144/7 e
256/7.
A proposição 35 do livro IX, o último dos três sobre teoria dos
números, contém uma formula para a soma de números em “progressão
geométrica”, expressa em termos elegantes mas poucos usuais:
“Se tantos números quantos quisermos estão em proporção
continuada, e se subtrai do segundo e último número iguais ao primeiro, então
assim como o excesso do segundo está para o primeiro, o excesso do último
estará para todos os que o precedem”.
Esse enunciado, é claro , é equivalente à fórmula:
an+1 – a1 = a2 – a1
a1 + a2 +...+an = a1
que por sua vez eqüivale a:
Sn= a – arn
1 - r
Página do livro Os Elementos
Na Matemática grega depois de Euclides surgiu o seguinte
problema: “Se a², b², c² estão em Progressão Aritmética, então b + c, c + a, a +
b estão em progressão harmônica”.
Diofanto de Alexandria (século III d. C.) teve uma importância
enorme para o desenvolvimento da álgebra e uma grande influência sobre os
europeus. Ele escreveu três trabalhos, sendo o mais importante a Aritmética,
que era composta por treze livros.
A Aritmética é uma abordagem analítica da teoria algébrica dos
números que eleva o autor à condição de gênio em seu campo. Dos problemas
que encontram-se em Aritmética, pode-se dizer que todos eles são atraentes e
alguns instigantes, e deve-se ter em mente que para Diofanto, número significa
número racional positivo.
O problema 7 do livro III é o seguinte: “Encontre três números em
Progressão Aritmética, sabendo-se que a soma de dois quaisquer deles é um
quadrado. Segundo Diofanto, a resposta é 120 ½, 840 ½, 1560 ½).Em 1202,
Leonardo de Pisa (Fibonacci = filius Bonacci) matemático e comerciante da
idade média, escreveu um livro denominado Liber Abacci, que chegou a nós,
graças à sua segunda edição datada de 1228. Este livro contém uma grande
quantidade de assuntos relacionados com a Aritmética e Álgebra da época e
realizou um papel importante no desenvolvimento matemático na Europa nos
séculos seguintes pois por este livro que os europeus vieram a conhecer os
algarismos hindus, também denominados arábicos.
A teoria contida no livro Liber Abacci é ilustrada com muitos
problemas que representam uma grande parte do livro. Um dos problemas que
pode ser encontrado nas páginas 123-124 deste livro é o problema dos pares
de coelhos (paria coniculorum).
Problema dos pares de coelhos: Quantos pares de coelhos
podem ser gerados de um par de coelhos em um ano? Um homem tem um par
de coelhos em um ambiente inteiramente fechado. Desejamos saber quantos
pares de coelhos podem ser gerados deste par em um ano, se de um modo
natural a cada mês ocorre a produção de um par e um par começa a produzir
coelhos quando completa dois meses de vida.
Tal processo continua através dos diversos meses até completar
um ano. Observa-se esta formação no gráfico
com círculos, mas também pode-se perceber que
a sequência numérica, conhecida como a sequência de Fibonacci, indica o
número de pares ao final de cada mês:
1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Os hindus também foram hábeis aritméticos e deram
contribuições significativas à álgebra, somando Progressões Aritméticas e
Geométricas rapidamente. Os problemas de aritmética hindus comumente
Leonardo de Pisa
envolviam irracionais quadráticos, o teorema de Pitágoras, Progressões
Aritméticas e permutações.
O Matemático hindu mais importante do século doze foi Bhaskara
(1114 a cerca de 1185). Ele foi também o último matemático medieval
importante da Índia, e sua obra representa a culminação de contribuições
hindus anteriores.
O seu tratado mais conhecido, o “lilavati”, recebeu o nome de sua
filha, afim de consolar a infeliz moça que perdeu a oportunidade de se casar
por causa da confiança de seu pai em sua predições astrológicas. Tanto o
“lilavati” quanto o “vija-ganita”, contém numerosos problemas sobre os tópicos
favoritos dos hindus: equações liniares e quadradáticas, tanto determinadas
quanto indeterninadas, simples mensuração, “progressões aritméticas e
geométricas”, radicais, tríadas pitagóricas e outros. Um deles cita o seguinte
problema:
“Numa expedição para calcular os elefantes de seu inimigo, um
rei marchou 2 yojanas no primeiro dia. Diga, calcular inteligentemente, a razão
com que sua marcha diária aumentou, se ele alcançou a cidade do inimigo, a
uma distância de 80 yojanas, em uma semana?
A Matemática na Europa conta a história de Michael Stifel (1486-
1567) que é considerado o maior algebrista alemão do século XVI. Sua obra
matemática mais conhecida é “Arithmética” integra, publicada em 1944 e
dividida em três partes, números racionais, números irracionais e álgebra. Na
primeira parte, ou seja, na parte dos números racionais, Stifel salienta as
vantagens de se associar uma “progressão aritmética” a uma “geométrica”.
Por volta de 1590, Napier revelou possuir completo conhecimento
da correspondência entre progressões aritméticas e geométricas, que o levou
aos logaritmos gerando em conseqüência de sua descoberta, e passando
diligentemente, a construção das tabelas de logaritmos que foram publicadas
vinte e quatro anos após.
Como sabemos hoje, o poder dos logaritmos como instrumentos
de cálculo repousa no fato de que eles reduzem multiplicações e divisões a
simples operações de adição e subtração. No entanto, na alvorada da
matemática moderna, a abordagem de John Napier (1550-1617) para eliminar
o fantasma das longas multiplicações e divisões difere consideravelmente das
longas prostaférese (palavra grega que significa “adição e subtração”), e se
baseia no fato de que, associando-se aos termos de uma progressão
geométrica:
b, b², b³,b4,..., bm, ..., bn, ...
aos da progressão aritmética:
1, 2, 3, 4, ..., m, ..., n, ...,
então o produto bm bn =bm+n de dois termos de primeira
progressão está associado à soma m+n dos termos correspondentes da
segunda progressão. Para manter os termos da “progressão geométrica”
suficientemente próximo do modo que se possa usar interpolação para
preencher as lacunas entre os termos da correspondência precedente, deve-se
escolher o número b bem próximo de 1.
Abraham De Moivre (1667-1754) era um huguenote francês que
buscou abrigo no clima politicamente mais ameno de Londres, depois da
revogação do edito de Nantes em 1685. De Moivre ganhava a vida na
Inglaterra como professor particular e tornou-se amigo íntimo de Issac Newton.
Há uma lenda interessante envolvendo a morte De Moivre.
Segundo ela, De Moivre teria revelado, certa ocasião, que daí para frente teria
que dormir, em cada dia, quinze

minutos a mais do que no dia
precedente. E quando essa “progressão
aritmética” atingiu 24horas ele de fato
teria morrido.
Johann Friederich Carl
Gauss nasceu em Brunswick,
Alemanha, em 30 de Abril de 1777. De
família humilde mas com o incentivo de
sua mãe, obteve brilhantismo na sua
carreira.
Gauss deu sinais de ser um gênio antes dos três anos de
idade. Nesta idade aprendeu a ler e a fazer
cálculos aritméticos mentalmente.
Aos dez anos de idade, durante
uma aula de matemática seu professor pediu para que todos os alunos
Carl Friedrich Gauss(1777 – 1855)obtivessem a soma dos números de 1 a 100. Em poucos minutos Gauss apresentou o resultado correto. Até então, ninguém era capaz desse feito. Ele se baseou no fato de que a soma dos números opostos é sempre constante
como mostra a figura:
Então ele multiplicou a constante (101) pelo número de termos e
dividiu pela metade, chegando a fórmula da soma da progressão aritmética:

Na doutrina de Darwin também podemos encontrar as

Progressões Aritméticas e Geométricas. O Darwinismo – teoria estudada em
Biologia, criada por Charles Robert Daewin.
Num dos quatro itens
fundamentais da doutrina de Darwin,
podemos encontramos uma referência
às Progressões Geométricas e
Aritméticas, uma influência das idéias de
Thomas Malthus, famoso economista.
Diz o item:
“As populações crescem
em P.G. ao mesmo tempo em que as
reservas alimentares para elas crescem
apenas em P. A.”
Em conseqüência deste
item, Darwin afirmou que “devido a tal
desproporção, os indivíduos empenhar-
2
S (a1 a ) n + n ⋅
=
se-iam numa luta pela vida, ao final da qual seriam selecionados os mais fortes
ou os mais aptos – a seleção natural – de alguns indivíduos em detrimento de
muitos outros”.
A comparação de Malthus entre o crescimento populacional e as
reservas alimentares não é mais aceita atualmente, pois, apesar da maior taxa
de crescimento populacional, não há uma desproporção tão grande como
mostra o diagrama.
CONCEITO DE SEQÜÊNCIAS E PROGRESSÕES
SEQÜÊNCIAS
Na lista de chamada de uma classe, o nome de cada aluno está
associado a um número natural não-nulo. Por exemplo:
1. Alberto Vieira de Moraes
2. Alessandra Rodrigues Fontana
3. Alex Stanley
.
.
.
30. Valdir de Souza Ramos
Quando associamos os números naturais 1, 2, 3, ... , 30 aos
elementos do conjunto B, dos alunos, de modo que cada um dos números – 1,
2, 3, ..., 30 – esteja associado a um único elemento de B, estamos
estabelecendo uma seqüência, em que:
• o número 1 é associado ao primeiro elemento da seqüência;
• o número 2 é associado ao segundo elemento da seqüência;
• o número 3 é associado ao terceiro elemento da seqüência;
.
.
.
• o número 30 é associado ao trigésimo elemento da seqüência.
Para representar uma seqüência, escrevemos entre parênteses
os seus elementos separados um a um por vírgulas, de modo que da esquerda
para a direita tenhamos: (primeiro elemento, segundo elemento, terceiro
elemento, ...).
Dessa maneira, a seqüência da lista de chamada fica
representada assim:
(Alberto Vieira de Moraes,
Primeiro elemento
Alessandra Rodrigues Fontana,
Segundo elemento
Alex Stanley, ...,
Terceiro elemento
Valdir de Souza Ramos)
Trigésimo elemento
Seqüência é todo conjunto cujos elementos obedecem a uma
determinada ordem.
Existem também seqüências infinitas como, por exemplo, a
seqüência dos números naturais pares em ordem crescente: (0, 2, 4, 6, 8,...).
Vale lembrar que:
�� Cada elemento de uma seqüência também pode ser denominado
de termo da seqüência.
�� Em uma seqüência, o termo que ocupa a posição de número n é
indicado pelo símbolo na. Isto é:
a1 indica o primeiro termo da seqüência;
a2 indica o segundo termo da seqüência;
a3 indica o terceiro termo da seqüência;
.
.
.
an indica o enésimo termo da seqüência.
�� Uma seqüência (a1, a2, a3, ... , an, ...), pode ser representada
abreviadamente por (an).
EXEMPLO:
Na seqüência ( 3, 7, 11, 15, ...) temos:
a1 = 3, a2 = 7, a3 = 11, a4 = 15, ...
�� Numa seqüência finita (a1, a2, a3, ... , an, ...), os termos a1 e an são
chamados de extremos da seqüência. Dois termos ai aj são
eqüidistantes dos extremos se, e somente se, o número de termos que
antecedem a1 é igual ao número de termos que sucedem aj.
EXEMPLO:
Na seqüência (a1, a2, a3, a4, ..., a58, a59, a60, a61), os extremos são
a1 e a61. Os termos a4 e a58 são eqüidistantes dos extremos.
�� Um termo am, é chamado de termo médio de uma seqüência com
número ímpar de termos se, e somente se, a quantidade de termos que
antecedem am é igual à quantidade de termos que o sucedem. No
exemplo do item anterior, o termo médio é a31.
LEI DE FORMAÇÃO DE UMA SEQÜÊNCIA:
Um conjunto de informações capazes de determinar todos os
termos de uma seqüência e a ordem em que se apresentam é chamado de lei
de formação da seqüência.
EXEMPLO:
a) Considere a seguinte seqüência:
a n tal que a1 = 5
a n + 1 = 2 + a n
As informações a1 = 5 e a n + 1 = 2 + a n, determinam todos os
termos da seqüência e a ordem em que se apresentam. Vejamos:
O primeiro termo da seqüência é 5; isto é, a1 = 5;
Na igualdade a n + 1 = 2 + a n , atribuindo-se a n os valores 1, 2, 3,
..., obtemos os demais termos da seqüência, isto é:
n= 1 �� a2 = 2 + a1 ∴a2 = 2 + 5 ∴a2 = 7
n= 2 �� a3 = 2 + a2 ∴a3 = 2 + 7 ∴ a3 = 9
n= 3 �� a4 = 2 + a3 ∴a4 = 2 + 9 ∴ a4 = 11
.
.
Logo, a seqüência é (5, 7, 9, 11, ...).
PROGRESSÃO ARITMÉTICA (PA)
1. Definição:
A progressão aritmética é um tipo de seqüência bastante presente
no nosso cotidiano, como mostra a situação descrita a seguir.
Quando a quantidade de água de um reservatório atinge o mínimo
de 5m3, é aberto um registro, automaticamente, despejando-se 4m3 de água
por hora neste reservatório, até completar sua capacidade, que é de 45m3. A
seqüência a seguir apresenta a quantidade, em m3, contida no reservatório, de
hora em hora, a partir do instante que foi atingida a quantidade mínima:
(5,9,13,17,21,25,29,33,37,41,45)
Essa seqüência numérica é chamada de progressão aritmética
(PA), porque adicionando-se uma mesma constante a cada termo, obtém-se o
termo seguinte. (Neste caso a constante adicionada é o 4).
Progressão aritmética é toda seqüência numérica em cada termo,
a partir do segundo, é igual à soma do termo precedente (anterior) com uma
constante r. O número r é chamado de razão da progressão aritmética.
EXEMPLOS:
a) A seqüência (5,9,13,17,21,25,29,33,37,41,45) é uma PA finita de razão
4.
b) (10,8,6,4,2,0,-2,-4,...) é uma PA infinita de r=-2.
c) (5,5,5,5,...) é uma PA infinita de razão r=0.
2. Classificação das progressões aritméticas:
2.1 Crescente
Uma PA é crescente quando cada termo, a partir do segundo, é
maior que o termo que o antecede. Para que isso aconteça, é necessário e
suficiente que a razão seja positiva.
EXEMPLO:
(7,11,15,19,...) é uma PA crescente . Note que a razão é positiva, r= 4.
2.2 Decrescente
Uma PA é decrescente, quando em cada termo, a partir do
segundo, é menor que o termo que o antecedente. Para que isso aconteça, é
necessário e suficiente que a razão seja negativa.
EXEMPLO:
(50,40,30,20,...) é uma PA decrescente. Note que sua razão é negativa,
r= -10.
2.3 Constante
Uma PA é constante quando todos os seus termos são iguais.
Para que isso aconteça, é necessário e suficiente que a razão seja igual a zero.
EXEMPLO:
A PA (4/3, 4/3, 4/3,...) é constante. Note que sua razão é igual a zero, r=
0.
3. Termo geral de uma Progressão aritmética
Voltando à situação descrita na introdução, vimos que a PA:
(5,9,13,17,21,25,29,33,37,41,45)
Apresenta a quantidade de água, em m3, contida no reservatório,
de hora em hora, a partir do instante em que foi atingida a quantidade mínima.
Observe que podemos calcular a quantidade de água contida no
reservatório, no final de cada hora, adicionando à quantidade mínima (5m3) o
produto do número de horas pela vazão do registro (4m3/h). Por exemplo, para
calcular a quantidade de metros cúbicos de água contida no reservatório, 6
horas após a abertura do registro, basta efetuar:
5+6.4
Note que o resultado é o 7º termo da PA e, que
a1= 5 e r = 4, isto é
a7= a1+ 6r
Raciocinando de modo análogo, temos:
a8= a1+ 7r; a9= a1+ 8r, etc.
Essa idéia pode ser generalizada para qualquer PA, como
veremos a seguir.
Consideremos a PA de razão r:
(a1, a2, a3, a4, a5,...,an,....)
Qualquer termo dessa P.A. pode ser representada em função de
a1 r , observe:
(a1 + 0r; a1+ 1r, a1+ 2r, a1+ 3r,...),
Isto quer dizer, que qualquer termo na é igual à soma de a1 com o
produto (n-1)r, ou seja, a fórmula do termo geral da PA pode ser expressa:
an= a1+ (n-1)r
4. Termos eqüidistantes dos extremos de uma PA
Numa PA finita, a soma de dois termos eqüidistantes dos
extremos é igual à soma dos extremos.
5. Soma dos n primeiros termos de uma PA
Em uma pequena escola do principado de Braunschweig,
Alemanha, em 1785, o professor Buttner propôs a seus alunos que somassem
os números naturais de 1 a 100. Apenas três minutos depois, um gurizote de
oito anos aproximou-se da mesa do professor e, mostrando-lhe sua prancheta,
proclamou: “Aí está”. O professor, assombrado, constatou que o resultado
estava correto.
Aquele menino viria a ser um dos maiores matemáticos de todos
os tempos: Karl Friedrich Gauss (1777-1855). O cálculo efetuado foi simples e
elegante: ele percebeu que a soma do primeiro número, 1, com o último, 100, é
igual a 101; a soma do segundo número, 2, com o penúltimo, 99, é igual a 101;
também a soma do terceiro número, 3, com o antepenúltimo, 98, é igual a 101;
concluindo assim que a soma de dois termos eqüidistantes dos extremos é
igual à soma dos extremos.
TEOREMA:
A soma Sn dos n primeiros termos da PA (a1, a2, a3,...an..) é dada
por:
PROGRESSÃO GEOMÉTRICA (PG)
1. Definição:
Progressão geométrica é toda seqüência numérica em que cada
termo, a partir do segundo, é igual ao produto do termo precedente (anterior)
por uma constante q. O número q é chamado de razão da progressão
geométrica.
Várias situações do nosso cotidiano ou do universo científico
relacionam grandezas que crescem ou decrescem pelo produto por uma
constante. O estudo dessas grandezas exige o conhecimento de um tipo
especial de seqüência chamada de progressão geométrica. A seguir é
apresentada uma dessas situações.
Um capital de R$ 10.000,00 é aplicado durante cinco anos à taxa
de juro composto de 20% ao ano. A seguir apresenta os montantes, em reais,
ano a ano, a partir do início da aplicação:
(10.000, 12.000,14.400,17.280,20.736)
Essa seqüência é numérica é chamada de progressão geométrica
(PG), porque, multiplicando-se cada termo por uma mesma constante, obtémse
o termo seguinte. (Nesse caso, multiplicou-se cada termo constante 1,2.)
2
Sn (a1 an).n
+
=
EXEMPLOS:
a) (3,6,12,24,48,96) é uma PG finita de razão q= 2.
b) (1, ½, ¼, 1/8, 1/16,...) é uma PG infinita de razão q= ½.
c) (2, -6, 18, -54, 162,...) é uma PG infinita de razão q= -3.
d) (5, 0, 0, 0,...) é uma PG infinita de razão q= 0.
e) (0, 0, 0,...) é uma PG infinita de razão indeterminada.
2. Classificação das progressões geométricas.
2.1 Crescente
Uma PG é crescente quando cada termo, a partir do segundo, é
maior que o termo que antecede. Para que isso aconteça, é necessário e
suficiente que a1>0 e q>1, ou a1<0 e 0< q <1.
EXEMPLOS:
a) (4, 8, 16, 32,...) é uma PG crescente de razão q=2.
b) (-4, -2, -1, -1/2,...) é uma PG crescente de razão q=1/2.
2.2 Decrescente
Uma PG é decrescente quando cada termo, a partir do segundo,
é menor que o termo que o antecede. Para que isso aconteça, é necessário e
suficiente que a1>0 e 0 < q <1, ou a1<0 e q>1.
EXEMPLOS:
a) (8, 4, 2, 1, ½, ..., ) é uma PG decrescente de razão q= ½.
b) (-1, -2, -4, -8, ...) é uma PG decrescente de razão q= 2.
2.3 Constante
Uma PG é constante quando os seus termos são iguais. Para que
isso aconteça, é necessário e suficiente que sua razão seja 1 ou que todos os
seus termos sejam nulos.
EXEMPLOS:
a) (8, 8, 8, ...) é uma PG constante de razão q= 1.
b) (0, 0, 0, 0,....) é uma PG constante de razão indeterminada.
2.4 Oscilante
Uma PG é oscilante quando todos os seus termos são diferentes
de zero e dois termos consecutivos quaisquer têm sinais opostos. Para que
isso aconteça, é necessário e suficiente que a1≠0 e q< 0.
EXEMPLOS:
a) (3, -6, 12, -24, 48, -96,...) PG oscilante de razão q= -2.
b) (-1, ½, -1/4, 1/8, -1/16,...) é uma PG oscilante de razão q= -
1/2.
2.5 Quase nula
Uma PG é quase nula quando o primeiro termo é diferente de
zero e todos os demais são iguais a zero. Para que isso aconteça, é necessário
e suficiente que a1≠ 0 e q= 0.
EXEMPLO:
(8, 0, 0, 0,....) é uma PG quase nula.
2.6 Propriedade
Uma seqüência de três termos, em que o primeiro é diferente de
zero, é a PG se, somente se, o quadrado do termo médio é igual ao produto
dos outros dois, isto é, sendo a≠ 0, temos:
(a, b, c) é PG -�� b2= a.c.
3. Soma dos n primeiros termos de uma PG
A taxa de crescimento anual na produção de soja de um estado
brasileiro é de 5%. Para estimar o total de soja produzida nesse estado e trinta
anos, de 2001 a 2030, o secretário da agricultura supôs que essa taxa
permaneça constante a partir da produção de 2001, que foi 4 milhões de
toneladas. Essa estimativa é a soma dos termos da seguinte PG de trinta
termos e razão 1,05:
(4, 4,2; 4,41;...4. (1,05)27; 4. (1,05)28; 4. (1,05)29) em que cada
termo representa a quantidade de soja produzida anualmente, em milhões de
toneladas.
Mesmo dispondo de uma calculadora, o secretário não somou os
termos um a um, pois o trabalho seria longo e tedioso. Ele usou a fórmula a
seguir, que calcula a soma dos n primeiros termos de uma PG não- constante,
com os primeiro termo a1 e a razão q:
Generalizando, veremos a seguir, que existe o limite da soma dos
infinitos termos de qualquer PG cuja razão q obedeça à condição: -1< q< 1.
O limite Sn da soma dos infinitos termos de uma PG (a1, a2, a3,...),
de razão q, -1< q< 1, é dado por:
q
Sn a q
n
−
−
=
1
.(1 ) 1
Notas
- Existe o limite da soma dos infinitos termos de uma PG de razão
q, se, e somente se, -1< q< 1.
- O limite da soma dos infinitos termos de uma PG é chamado,
simplesmente, de soma dos infinitos termos da PG.
APLICAÇÕES PRÁTICAS DAS PROGRESSÕES
As progressões aritméticas e geométricas estudadas nos
capítulos I e II são modelos matemáticos cujas aplicações nos ajudaram a
entender muitos fenômenos em diversos ramos da atividade humana. Em
resumo, as progressões também são conceitos, cujo ensino pode ser
diferenciado.
Os exemplos a seguir nos revelam, onde podemos encontrar as
progressões aritméticas e geométricas:
EXEMPLO I:
Fazendo um teste com um automóvel nacional, verificamos que o
mesmo acelera de 0 a 60 Km/h em 6 segundos. Admitindo que a aceleração do
automóvel seja constante, concluímos que, após a partida, a sua velocidade
aumenta de 10 km/h a cada segundo. A tabela mostra a velocidade associada
ao tempo.
Tempo (s) Velocidade (Km/h)
0 0
1 10
2 20
q
S a
−
= ∞ 1
1
3 30
4 40
5 50
6 60
Os números que representam as velocidades do automóvel
formam a seguinte seqüência ou sucessão (0,10,20,30,40,50,60). Sucessões
como essa, cuja diferença entre qualquer termo e o seu antecessor é
constante, são chamadas de progressões aritméticas, e além do mais
caracterizada como crescente.
Aproveitando o mesmo exemplo, podemos perceber que após ter
atingido os 60 Km/h, o automóvel terá de frenar, assim reduzindo sua
velocidade até 0 Km/h em 6 segundos. Admitindo que a desaceleração do
mesmo seja constante, a velocidade caíra 10 Km/h em cada segundo. Dessa
forma teremos a seguinte tabela:
Tempo (s) Velocidade (Km/h)
0 60
1 50
2 40
3 30
4 20
5 10
6 0
Dessa forma, os números que representam as velocidades do
automóvel (60,50,40,30,20,10,0) formam, nesta ordem, uma progressão
aritmética decrescente.
EXEMPLO II:
Um atleta em fase de treinamento, prepara-se pra voltar á prática
esportiva de ciclismo depois de um tempo que ficou afastado. No entanto ele
mesmo sabe que não pode pedalar a mesma quantia de quilômetros como
antigamente, ou seja, ele tem que realizar um treinamento mantendo um
crescimento constante. Vejamos na tabela abaixo como ele planejou o
treinamento:
PERÍODO DISTÂNCIA
1º dia 5 Km
2º dia 10 Km
3º dia 13 Km
4º dia 16 Km
5º dia 19 Km
... ...
Segundo seu planejamento ele deseja um aumento constante a
partir do segundo dia. Sabendo que o mesmo atleta pretende fazer o
treinamento num período de 12 dias, vejamos como ele pode obter a
quilometragem final de seu treinamento:
POSSÍVEL RESOLUÇÃO:
As distâncias percorridas diariamente pelo atleta formam a
seqüência (5,10,13,16,19,...) e, a partir do 2º termo, a seqüência é uma
progressão aritmética. A soma das distâncias percorridas, St, é dada por
St=5+S11; S11 é a soma dos termos da progressão aritmética, em que a1=10,
r=3 e n=11.
Temos:
S11 = (a1+a11) 11
2
�� S11 = (10+a11) 11
2
Como a11 = a1 + 10 r �� a11 = 10 + 10 . 3 �� a11 = 40; então:
S11 = (10 + 40) 11
2
�� S11 = 275
Portanto, St = 5+275 �� St = 280
Ou seja, o atleta irá percorrer 280 Km nos 12 dias de treinamento.
EXEMPLO III:
A companhia que administra uma rodovia quer colocar radares
eletrônicos de controle de velocidade ao longo de 500 quilômetros. Dessa
forma, segue a tabela com os seguintes dados:
Radar Quilômetro
primeiro 10
segundo 50
terceiro 90
E assim sucessivamente formando uma progressão aritmética.
Sendo assim, a companhia quer saber: Quantos radares eletrônicos serão
colocados no trecho planejado?
POSSÍVEL RESOLUÇÃO:
Se dermos uma olhada na tabela acima podemos nos deparar
que de um radar para o outro os quilômetros aumentam de 40 em 40, então
poderíamos fazer a seguinte conta:
2º radar �� 10+40 = 50
3º radar �� 50+40 = 90
4º radar �� 90+40 = 130
5º radar �� 130+40 = 170
6º radar �� 170+40 = 210
7º radar �� 210+40 = 250
8º radar �� 250+40 = 290
9º radar �� 290+40 = 330
10º radar �� 330+40 = 370
11º radar �� 370+40 = 410
12º radar �� 410+40 = 450
13º radar �� 450+40 = 490 sendo assim, chegaríamos a conclusão de que no
quilômetro 490 seria colocado o décimo terceiro radar, então chegaríamos na
resposta de 13 radares no trecho planejado da rodovia.
Mas, há uma forma muito mais simples e objetiva de se chegar na
resposta que vamos apresentar pra vocês que seria o método pela fórmula:
RESOLUÇÃO PELA FÓRMULA:
a1 = 10
r = 40
n = número de radares e n ∈I Ν
Supondo que an = 500, temos:
an = a1 + (n – 1).r
500 = 10 + (n – 1).40
500 = 10 + 40n – 40
530 = 40n
n =
40
530
n = 13,25
Como n ∈ I Ν , n = 13
Logo, a companhia deverá colocar 13 radares.
Se quisermos saber em qual quilômetro será colocado o décimo
terceiro radar, voltamos a fórmula e substituímos o n por 13:
an = a1 + (n – 1).r
an = 10 + (13 – 1).40
an = 10 + 480
an = 490, será colocado no quilômetro 490.
EXEMPLO IV:
Num treino de basquete pode se observar que um garoto fez 1
cesta no 1º dia, 2 cestas no 2º dia, 4 cestas no 3º dia, e assim sucessivamente.
Quantas cestas este garoto fará no 10º dia?
POSSÍVEL RESOLUÇÃO:
PG (1, 2, 4, ..., an) �� Progressão Finita
temos: a1 = 1
q = 2
n = 10
Para determinar a10, fazemos:
Fórmula do termo geral: an=a1.qn-1
então: a10 = a1.q9
a10 = 1.29
a10 = 512
Assim, podemos concluir que este garoto fará 512 cestas no 10º
dia de treino.
EXEMPLO V:
Num jogo de basquete, pudemos observar que com 10 minutos
de jogo o time A tinha 4 pontos marcados no placar, com 20 min de jogo o
mesmo time tinha 8 pontos, com 30 min tinha 16 pontos e assim
sucessivamente. Ao término do jogo, que tem duração de 60 min, qual será a
pontuação do time A?
POSSÍVEL RESOLUÇÃO:
PG (4, 8, 16, ..., an)�� Progressão Finita
Temos: a1 = 4
q = 2
n = 6
Para determinar a6, fazemos:
Fórmula do termo geral: an=a1.qn-1
Então: a6 = a1.a5
a6 = 4.25
a6 = 4.32
a6 = 128
Assim, podemos concluir que o time A terá 128 pontos ao término
do jogo.
EXEMPLO VI:
Em uma experiência de laboratório, um frasco recebe, no primeiro
dia do mês, 3 gotas de um determinado líquido; no segundo dia recebe 9 gotas;
no terceiro dia recebe 27 gotas; e assim por diante. No dia em que recebeu
2187 gotas ficou completamente cheio. Em que dia do mês isso aconteceu?
POSSÍVEL RESOLUÇÃO:
PG (3, 9, 27, ..., 2187) �� Progressão Finita
Temos: a1=3
q=3
an=2187
Agora, temos que calcular n, que é correspondente ao número do
dia do mês que acontece o fato:
Fórmula do termo geral: an=a1.qn-1
Então: 2187=3.3n-1
3n-1=2187
3
3n-1=729
3n-1=36
n-1=6
n= 6+1
n=7
Assim, podemos concluir que no 7º dia o frasco recebeu 2187
gotas e ficou totalmente cheio.
EXEMPLO VII:
Uma pessoa aposta na loteria durante cinco semanas, de tal
forma que, em cada semana, o valor da aposta é o dobro do valor da aposta da
semana anterior. Se o valor da aposta da 1ª semana é R$60,00, qual o valor
total apostado após as cinco semanas?
POSSÍVEL RESOLUÇÃO:
PG(60,...,an)�� Progressão Finita
Temos: a1=60
q=2
n=5
Como queremos o valor TOTAL apostado, usamos a fórmula da
soma de n termos de uma
PG finita:
Sn= a1.(qn-1)
q-1
S5= 60.(25-1) �� S5= 60.31 �� S5 = 1860
2-1
Assim, concluímos que esta pessoa gastou R$1860,00 em cinco
semanas de aposta.
CONSIDERAÇÕES FINAIS
Pode-se observar que mais uma vez a Matemática como um todo,
se mostra importante na medida em que a sociedade necessita e se utiliza dos
conhecimentos dessa área, que por sua vez são essenciais para a inserção
das pessoas como cidadãos no mundo do trabalho, da cultura e das relações
sociais.
Vê-se que os povos egípcios e os babilônicos se utilizavam
desses conceitos para conseguir aquilo que necessitavam. Em um caso
particular dos egípcios, eles procuravam estabelecer padrões para saberem
quando haveria inundação e assim garantir seus alimentos. Com certeza é de
grande valia a inserção dos contextos históricos em sala de aula, pois o
discente passa a ver a matemática como uma criação humana, enquanto o
docente cria condições para que o aluno desenvolva atitudes e valores mais
favoráveis diante desse conhecimento.
Em relação aos conceitos, houve a oportunidade de se ver as
demonstrações das mesmas, onde por si própria nos passa um melhor
entendimento sobre a validade das fórmulas.
No que diz respeito às aplicações dos conceitos em nosso
cotidiano, pudemos perceber a riqueza dos conceitos de progressões. Ao
mesmo tempo, pudemos ver a flexibilidade desses conceitos em diferentes
situações e assim validando uma das características principais para que se
assegure a aprendizagem: o real interesse do discente em aprender algo, é
quando aquilo serve ou servirá para alguma situação que ele necessitará. Se
pudermos assim fazer com que o discente construa melhor os conceitos, então
vale a pena disponibilizar de um tempo a mais para prepararmos algumas
aplicações.
Portanto, se faz necessário que os professores utilizem informações
desta natureza durante seu processo de ensino, para enfim satisfazer a
necessidade de uso imediato e prático dos conteúdos escolares, facilitando a
motivação do aluno e sua aprendizagem.
BIBLIOGRAFIA:
BOYER, Carl Benjamin. História da Matemática. São Paulo: Edgard
Blücher, 1974.
CARVALHO, Silva, COSTA, Maria Cecília. Padrões Numéricos e
Seqüências. São Paulo: Moderna, 1997.
EVES, Howard. Introdução à História da Matemática. Campinas: Esitor
da UNICAMP, 1995.
História da Álgebra. http://users.hotlink.com.br/marielli/matematica/
histomatica/histoalg.html. Acesso em 15/03/2004
KIYUKAWA, Rokusaburo, SMOLE, Kátia Cristina Stocco. Matemática. 2
ed.. São Paulo: Saraiva, 1999.
Malha Atlântica. http://www.malhatlantica.pt/mathis/index.html. Acesso
em 15/03/2004
Matemática Essencial. http://pessoal.sercomtel.com.br/matematica/.
Acesso em 15/03/2004
PAIVA, Manoel. Matemática. São Paulo: Moderna, 2003.
SANTOS, Carlos A. M. dos et al. Matemática. São Paulo: Ática, 2003.
 12
12 ESCOLA ESTADUAL DE ENSINO MÉDIO 9 DE MAIO - IMBÉ / RS / BRASIL
ESCOLA ESTADUAL DE ENSINO MÉDIO 9 DE MAIO - IMBÉ / RS / BRASIL